Wallet Recovery

Creating pairs of private and public keys is a crucial part of allowing Bitcoin wallets to receive and spend bitcoins. But losing access to a private key can make it impossible for anyone to ever spend the bitcoins received to the corresponding public key. Wallet and protocol developers over the years have worked to design systems that allow users to recover access to their bitcoins after a problem without compromising security the rest of the time.

In this chapter, we’ll examine some of the different methods employed by wallets to prevent the loss of data from becoming a loss of money. Some solutions have almost no downsides and are universally adopted by modern wallets. We’ll simply recommend those solutions as best practices. Other solutions have both advantages and disadvantages, leading different wallet authors to make different trade-offs. In those cases, we’ll describe the various options available.

Independent Key Generation

Wallets for physical cash hold that cash, so it's unsurprising that many people mistakenly believe that Bitcoin wallets contain bitcoins. In fact, what many people call a Bitcoin wallet—which we call a wallet database to distinguish it from wallet applications—contains only keys. Those keys are associated with bitcoins recorded on the blockchain. By proving to Bitcoin full nodes that you control the keys, you can spend the associated bitcoins.

Simple wallet databases contain both the public keys to which bitcoins are received and the private keys that allow creating the signatures necessary to authorize spending those bitcoins. Other wallets' databases may contain only public keys, or only some of the private keys necessary to authorize a spending transaction. Their wallet applications produce the necessary signatures by working with external tools, such as hardware signing devices or other wallets in a multisignature scheme.

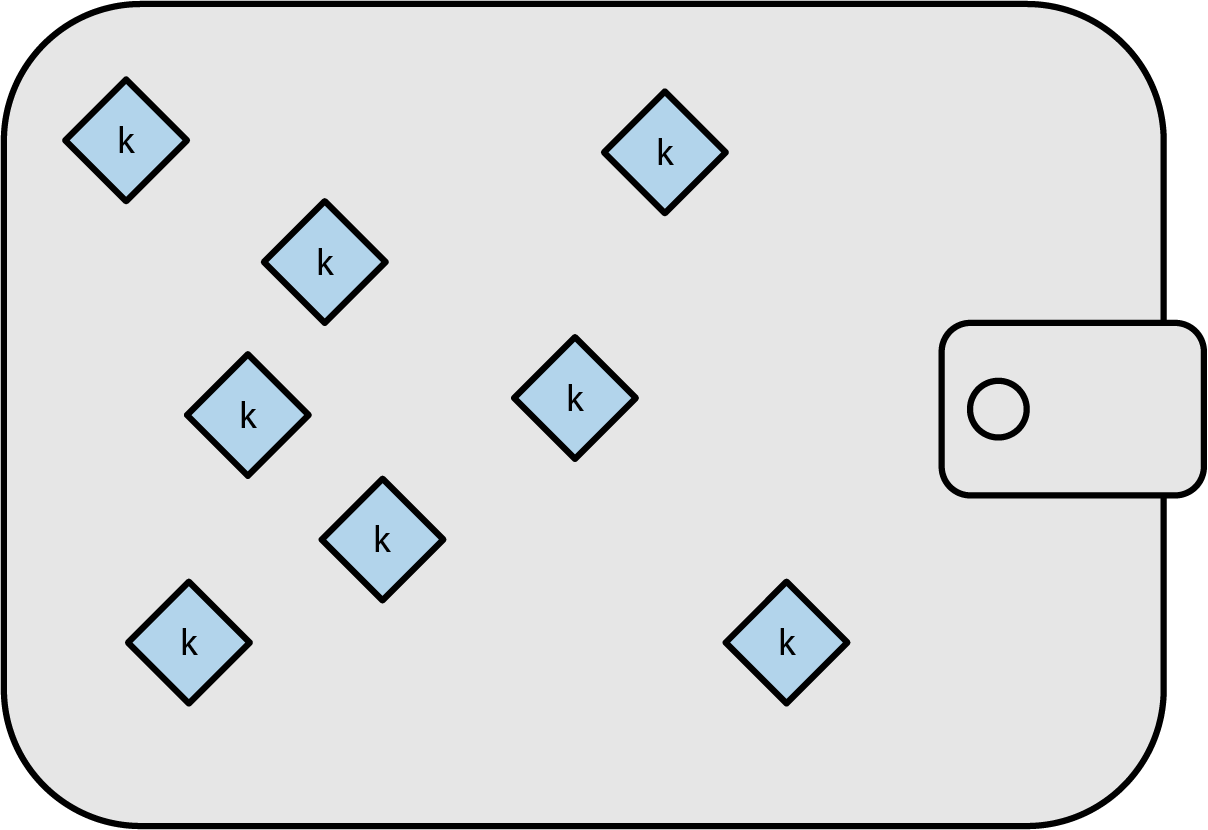
It’s possible for a wallet application to independently generate each of the wallet keys it later plans to use, as illustrated in Nondeterministic key generation: a collection of independently generated keys stored in a wallet database.. All early Bitcoin wallet applications did this, but it required users to back up the wallet database each time they generated and distributed new keys, which could be as often as each time they generated a new address to receive a new payment. Failure to back up the wallet database on time would lead to the user losing access to any funds received to keys that had not been backed up.

For each independently generated key, the user would need to back up about 32 bytes, plus overhead. Some users and wallet applications tried to minimize the amount of data that needed to be backed up by only using a single key. Although that can be secure, it severely reduces the privacy of that user and all of the people with whom they transact. People who valued their privacy and those of their peers created new key pairs for each transaction, producing wallet databases that could only reasonably be backed up using digital media.

Figure 1. Nondeterministic key generation: a collection of independently generated keys stored in a wallet database.

Modern wallet applications don’t independently generate keys but instead derive them from a single random seed using a repeatable (deterministic) algorithm.

Deterministic Key Generation

A hash function will always produce the same output when given the same input, but if the input is changed even slightly, the output will be different. If the function is cryptographically secure, nobody should be able to predict the new output—not even if they know the new input.

This allows us to take one random value and transform it into a practically unlimited number of seemingly random values. Even more useful, later using the same hash function with the same input (called a seed) will produce the same seemingly random values:

# Collect some entropy (randomness)
$ dd if=/dev/random count=1 status=none | sha256sum
f1cc3bc03ef51cb43ee7844460fa5049e779e7425a6349c8e89dfbb0fd97bb73  -

# Set our seed to the random value
$ seed=f1cc3bc03ef51cb43ee7844460fa5049e779e7425a6349c8e89dfbb0fd97bb73

# Deterministically generate derived values
$ for i in {0..2} ; do echo "$seed + $i" | sha256sum ; done
50b18e0bd9508310b8f699bad425efdf67d668cb2462b909fdb6b9bd2437beb3  -
a965dbcd901a9e3d66af11759e64a58d0ed5c6863e901dfda43adcd5f8c744f3  -
19580c97eb9048599f069472744e51ab2213f687d4720b0efc5bb344d624c3aa  -

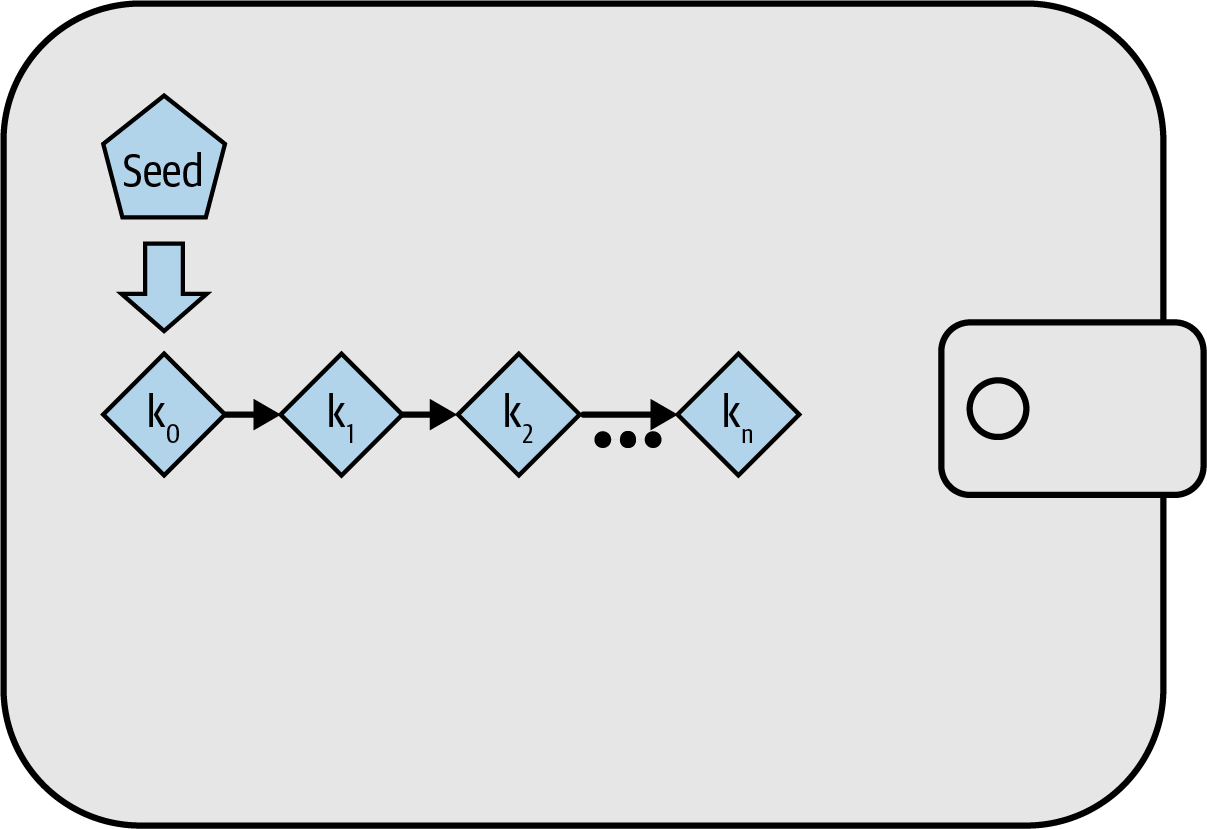
If we use the derived values as our private keys, we can later generate exactly those same private keys by using our seed value with the algorithm we used before. A user of deterministic key generation can back up every key in their wallet by simply recording their seed and a reference to the deterministic algorithm they used. For example, even if Alice has a million bitcoins received to a million different addresses, all she needs to back up in order to later recover access to those bitcoins is:

f1cc 3bc0 3ef5 1cb4 3ee7 8444 60fa 5049
e779 e742 5a63 49c8 e89d fbb0 fd97 bb73

A logical diagram of basic sequential deterministic key generation is shown in Deterministic key generation: a deterministic sequence of keys derived from a seed for a wallet database.. However, modern wallet applications have a more clever way of accomplishing this that allows public keys to be derived separately from their corresponding private keys, making it possible to store private keys more securely than public keys.

Figure 2. Deterministic key generation: a deterministic sequence of keys derived from a seed for a wallet database.

Public Child Key Derivation

In [public_key_derivation], we learned how to create a public key from a private key using elliptic curve cryptography (ECC). Although operations on an elliptic curve are not intuitive, they are analogous to the addition, subtraction, and multiplication operations used in regular arithmetic. In other words, it’s possible to add or subtract from a public key, or to multiply it. Consider the operation we used in [public_key_derivation] for generating a public key (K) from a private key (k) using the generator point (G):

$\begin{equation} {K = k \times G} \end{equation}$

It’s possible to create a derived key pair, called a child key pair, by simply adding the same value to both sides of the equation:

K + (123 \times G) == (k + 123) \times G

Tip

In equations throughout this book, we use a single equals sign for operations such as K = k × G where the value of a variable is calculated. We use a double equals sign to show both sides of an equation are equivalent, or that an operation should return false (not true) if the two sides aren’t equivalent.

An interesting consequence of this is that adding 123 to the public key can be done using entirely public information. For example, Alice generates public key K and gives it to Bob. Bob doesn’t know the private key, but he does know the global constant G, so he can add any value to the public key to produce a derived public child key. If he then tells Alice the value he added to the public key, she can add the same value to the private key, producing a derived private child key that corresponds to the public child key Bob created.

In other words, it’s possible to create child public keys even if you don’t know anything about the parent private key. The value added to a public key is known as a key tweak. If a deterministic algorithm is used for generating the key tweaks, then it’s possible for someone who doesn’t know the private key to create an essentially unlimited sequence of public child keys from a single public parent key. The person who controls the private parent key can then use the same key tweaks to create all the corresponding private child keys.

This technique is commonly used to separate wallet application frontends (which don’t require private keys) from signing operations (which do require private keys). For example, Alice’s frontend distributes her public keys to people wanting to pay her. Later, when she wants to spend the received money, she can provide the key tweaks she used to a hardware signing device (sometimes confusingly called a hardware wallet) that securely stores her original private key. The hardware signer uses the tweaks to derive the necessary child private keys and uses them to sign the transactions, returning the signed transactions to the less-secure frontend for broadcast to the Bitcoin network.

Public child key derivation can produce a linear sequence of keys similar to the previously seen Deterministic key generation: a deterministic sequence of keys derived from a seed for a wallet database., but modern wallet applications use one more trick to provide a tree of keys instead a single sequence, as described in the following section.

Hierarchical Deterministic (HD) Key Generation (BIP32)

Every modern Bitcoin wallet of which we’re aware uses hierarchical deterministic (HD) key generation by default. This standard, defined in BIP32, uses deterministic key generation and optional public child key derivation with an algorithm that produces a tree of keys. In this tree, any key can be the parent of a sequence of child keys, and any of those child keys can be a parent for another sequence of child keys (grandchildren of the original key). There’s no arbitrary limit on the depth of the tree. This tree structure is illustrated in HD wallet: a tree of keys generated from a single seed..

Figure 3. HD wallet: a tree of keys generated from a single seed.

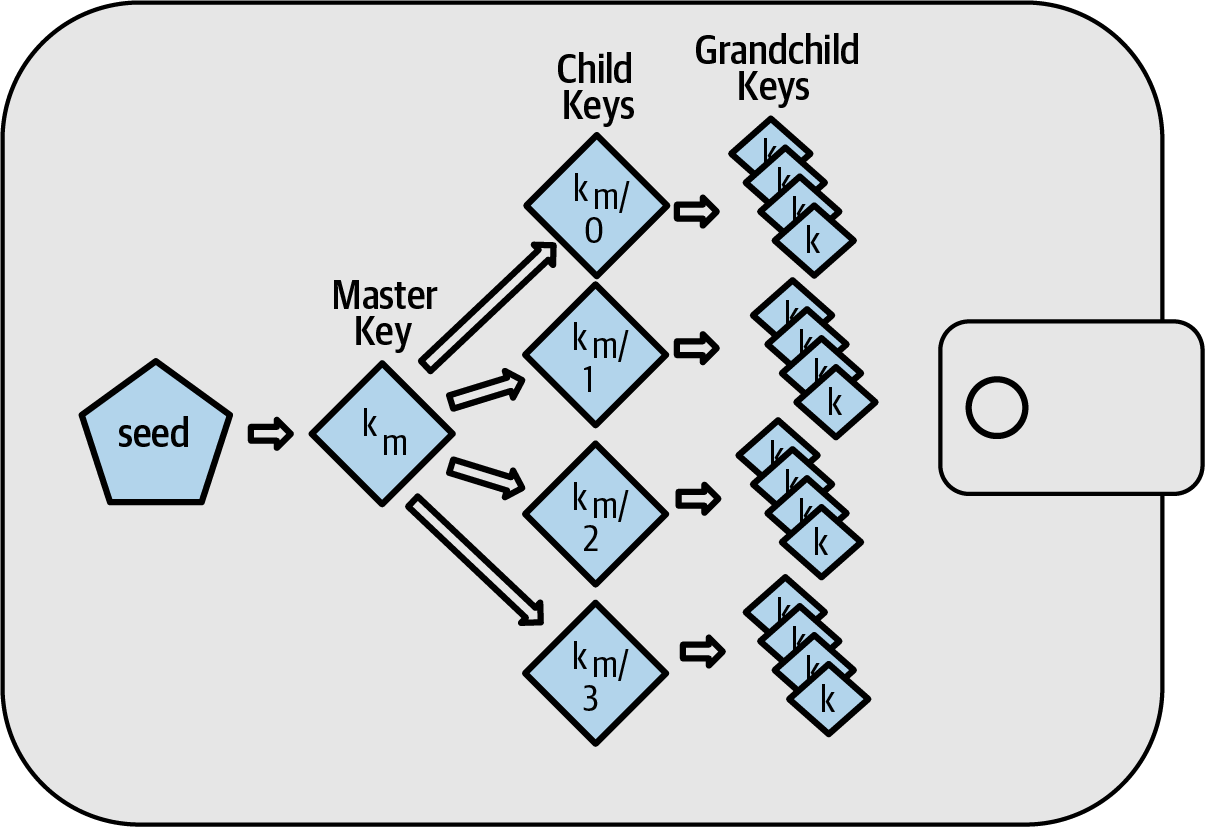
The tree structure can be used to express additional organizational meaning, such as when a specific branch of subkeys is used to receive incoming payments and a different branch is used to receive change from outgoing payments. Branches of keys can also be used in corporate settings, allocating different branches to departments, subsidiaries, specific functions, or accounting categories.

We’ll provide a detailed exploration of HD wallets in Creating an HD Wallet from the Seed.

Seeds and Recovery Codes

HD wallets are a very powerful mechanism for managing many keys all derived from a single seed. If your wallet database is ever corrupted or lost, you can regenerate all of the private keys for your wallet using your original seed. But, if someone else gets your seed, they can also generate all of the private keys, allowing them to steal all of the bitcoins from a single-sig wallet and reduce the security of bitcoins in multisignature wallets. In this section, we’ll look at several recovery codes, which are intended to make backups easier and safer.

Although seeds are large random numbers, usually 128 to 256 bits, most recovery codes use human-language words. A large part of the motivation for using words was to make a recovery code easy to remember. For example, consider the recovery code encoded using both hexadecimal and words in A seed encoded in hex and in English words.

Example 1. A seed encoded in hex and in English words

Hex-encoded:
0C1E 24E5 9177 79D2 97E1 4D45 F14E 1A1A

Word-encoded:
army van defense carry jealous true
garbage claim echo media make crunch

There may be cases where remembering a recovery code is a powerful feature, such as when you are unable to transport physical belongings (like a recovery code written on paper) without them being seized or inspected by an outside party that might steal your bitcoins. However, most of the time, relying on memory alone is dangerous:

If you forget your recovery code and lose access to your original wallet database, your bitcoins are lost to you forever.
If you die or suffer a severe injury, and your heirs don’t have access to your original wallet database, they won’t be able to inherit your bitcoins.
If someone thinks you have a recovery code memorized that will give them access to bitcoins, they may attempt to coerce you into disclosing that code. As of this writing, Bitcoin contributor Jameson Lopp has documented over 100 physical attacks against suspected owners of bitcoin and other digital assets, including at least three deaths and numerous occasions where someone was tortured, held hostage, or had their family threatened.

Tip	Even if you use a type of recovery code that was designed for easy memorization, we very strongly encourage you to consider writing it down.

Several different types of recovery codes are in wide use as of this writing:

BIP39: The most popular method for generating recovery codes for the past decade, BIP39 involves generating a random sequence of bytes, adding a checksum to it, and encoding the data into a series of 12 to 24 words (which may be localized to a user’s native language). The words (plus an optional passphrase) are run through a key-stretching function, and the output is used as a seed. BIP39 recovery codes have several shortcomings, which later schemes attempt to address.
Electrum v2: Used in the Electrum wallet (version 2.0 and above), this word-based recovery code has several advantages over BIP39. It doesn’t rely on a global word list that must be implemented by every version of every compatible program, plus its recovery codes include a version number that improves reliability and efficiency. Like BIP39, it supports an optional passphrase (which Electrum calls a seed extension) and uses the same key-stretching function.
Aezeed: Used in the LND wallet, this is another word-based recovery code that offers improvements over BIP39. It includes two version numbers: one is internal and eliminates several issues with upgrading wallet applications (like Electrum v2’s version number); the other version number is external, which can be incremented to change the underlying cryptographic properties of the recovery code. It also includes a wallet birthday in the recovery code, a reference to the date when the user created the wallet database. This allows a restoration process to find all of the funds associated with a wallet without scanning the entire blockchain, which is especially useful for privacy-focused lightweight clients. It includes support for changing the passphrase or changing other aspects of the recovery code without needing to move funds to a new seed—the user need only back up a new recovery code. One disadvantage compared to Electrum v2 is that, like BIP39, it depends on both the backup and the recovery software supporting the same word list.

Muun: Used in the Muun wallet, which defaults to requiring spending transactions be signed by multiple keys, this is a nonword code that must be accompanied by additional information (which Muun currently provides in a PDF). This recovery code is unrelated to the seed and is instead used to decrypt the private keys contained in the PDF. Although this is unwieldy compared to the BIP39, Electrum v2, and Aezeed recovery codes, it provides support for new technologies and standards that are becoming more common in new wallets, such as Lightning Network (LN) support, output script descriptors, and miniscript.
SLIP39: A successor to BIP39 with some of the same authors, SLIP39 allows a single seed to be distributed using multiple recovery codes that can be stored in different places (or by different people). When you create the recovery codes, you can specify how many will be required to recover the seed. For example, you create five recovery codes but only require three of them to recover the seed. SLIP39 provides support for an optional passphrase, depends on a global word list, and doesn’t directly provide versioning.

Note

A new system for distributing recovery codes with similarities to SLIP39 was proposed during the writing of this book. Codex32 allows creating and validating recovery codes with nothing except printed instructions, scissors, a precision knife, brass fasteners, and a pen—plus privacy and a few hours of spare time. Alternatively, those who trust computers can create recovery codes instantly using software on a digital device. You can create up to 31 recovery codes to be stored in different places, specifying how many of them will be required in order to recover the seed. As a new proposal, details about Codex32 may change significantly before this book is published, so we encourage any readers interested in distributed recovery codes to investigate its current status.

Recovery Code Passphrases

The BIP39, Electrum v2, Aezeed, and SLIP39 schemes may all be used with an optional passphrase. If the only place you keep this passphrase is in your memory, it has the same advantages and disadvantages as memorizing your recovery code. However, there’s a further set of trade-offs specific to the way the passphrase is used by the recovery code.

Three of the schemes (BIP39, Electrum v2, and SLIP39) do not include the optional passphrase in the checksum they use to protect against data entry mistakes. Every passphrase (including not using a passphrase) will result in producing a seed for a BIP32 tree of keys, but they won’t be the same trees. Different passphrases will result in different keys. That can be a positive or a negative, depending on your perspective:

On the positive, if someone obtains your recovery code (but not your passphrase), they will see a valid BIP32 tree of keys. If you prepared for that contingency and sent some bitcoins to the nonpassphrase tree, they will steal that money. Although having some of your bitcoins stolen is normally a bad thing, it can also provide you with a warning that your recovery code has been compromised, allowing you to investigate and take corrective measures. The ability to create multiple passphrases for the same recovery code that all look valid is a type of plausible deniability.
On the negative, if you’re coerced to give an attacker a recovery code (with or without a passphrase) and it doesn’t yield the amount of bitcoins they expected, they may continue trying to coerce you until you give them a different passphrase with access to more bitcoins. Designing for plausible deniability means there’s no way to prove to an attacker that you’ve revealed all of your information, so they may continue trying to coerce you even after you’ve given them all of your bitcoins.
An additional negative is the reduced amount of error detection. If you enter a slightly wrong passphrase when restoring from a backup, your wallet can’t warn you about the mistake. If you were expecting a balance, you will know something is wrong when your wallet application shows you a zero balance for the regenerated key tree. However, novice users may think their money was permanently lost and do something foolish, such as give up and throw away their recovery code. Or, if you were actually expecting a zero balance, you might use the wallet application for years after your mistake until the next time you restore with the correct passphrase and see a zero balance. Unless you can figure out what typo you previously made, your funds are gone.

Unlike the other schemes, the Aezeed seed encryption scheme authenticates its optional passphrase and will return an error if you provide an incorrect value. This eliminates plausible deniability, adds error detection, and makes it possible to prove that the passphrase has been revealed.

Many users and developers disagree on which approach is better, with some strongly in favor of plausible deniability and others preferring the increased safety that error detection gives novice users and those under duress. We suspect the debate will continue for as long as recovery codes continue to be widely used.

Backing Up Nonkey Data

The most important data in a wallet database is its private keys. If you lose access to the private keys, you lose the ability to spend your bitcoins. Deterministic key derivation and recovery codes provide a reasonably robust solution for backing up and recovering your keys and the bitcoins they control. However, it’s important to consider that many wallet databases store more than just keys—they also store user-provided information about every transaction they sent or received.

For example, when Bob creates a new address as part of sending an invoice to Alice, he adds a label to the address he generates so that he can distinguish her payment from other payments he receives. When Alice pays Bob’s address, she labels the transaction as paying Bob for the same reason. Some wallets also add other useful information to transactions, such as the current exchange rate, which can be useful for calculating taxes in some jurisdictions. These labels are stored entirely within their own wallets—not shared with the network—protecting their privacy and keeping unnecessary personal data out of the blockchain. For an example, see [alice_tx_labels].

Alice’s transaction history with each transaction labeled
Date	Label	BTC
2023-01-01	Bought bitcoins from Joe	+0.00100
2023-01-02	Paid Bob for podcast	−0.00075

However, because address and transaction labels are stored only in each user’s wallet database and because they aren’t deterministic, they can’t be restored by using just a recovery code. If the only recovery is seed-based, then all the user will see is a list of approximate transaction times and bitcoin amounts. This can make it quite difficult to figure out how you used your money in the past. Imagine reviewing a bank or credit card statement from a year ago that had the date and amount of every transaction listed but a blank entry for the "description" field.

Wallets should provide their users with a convenient way to back up label data. That seems obvious, but there are a number of widely used wallet applications that make it easy to create and use recovery codes but that provide no way to back up or restore label data.

Additionally, it may be useful for wallet applications to provide a standardized format to export labels so that they can be used in other applications (e.g., accounting software). A standard for that format is proposed in BIP329.

Wallet applications implementing additional protocols beyond basic Bitcoin support may also need or want to store other data. For example, as of 2023, an increasing number of applications have added support for sending and receiving transactions over the Lightning Network (LN). Although the LN protocol provides a method to recover funds in the event of a data loss, called static channel backups, it can’t guarantee results. If the node your wallet connects to realizes you’ve lost data, it may be able to steal bitcoins from you. If it loses its wallet database at the same time you lose your database, and neither of you has an adequate backup, you’ll both lose funds.

Again, this means users and wallet applications need to do more than just back up a recovery code.

One solution implemented by a few wallet applications is to frequently and automatically create complete backups of their wallet database encrypted by one of the keys derived from their seed. Bitcoin keys must be unguessable and modern encryption algorithms are considered very secure, so nobody should be able to open the encrypted backup except someone who can generate the seed. This makes it safe to store the backup on untrusted computers such as cloud hosting services or even random network peers.

Later, if the original wallet database is lost, the user can enter their recovery code into the wallet application to restore their seed. The application can then retrieve the latest backup file, regenerate the encryption key, decrypt the backup, and restore all of the user’s labels and additional protocol data.

Backing Up Key Derivation Paths

In a BIP32 tree of keys, there are approximately four billion first-level keys; each of those keys can have its own four billion children, with those children each potentially having four billion children of their own, and so on. It’s not possible for a wallet application to generate even a small fraction of every possible key in a BIP32 tree, which means that recovering from data loss requires knowing more than just the recovery code, the algorithm for obtaining your seed (e.g., BIP39), and the deterministic key derivation algorithm (e.g., BIP32)—it also requires knowing what paths in the tree of keys your wallet application used for generating the specific keys it distributed.

Two solutions to this problem have been adopted. The first is using standard paths. Every time there’s a change related to the addresses that wallet applications might want to generate, someone creates a BIP defining what key derivation path to use. For example, BIP44 defines m/44'/0'/0' as the path to use for keys in P2PKH scripts (a legacy address). A wallet application implementing this standard uses the keys in that path both when it is first started and after a restoration from a recovery code. We call this solution implicit paths. Several popular implicit paths defined by BIPs are shown in [bip_implicit_paths]

Implicit script paths defined by various BIPs
Standard	Script	BIP32 path
BIP44	P2PKH	`m/44'/0'/0'`
BIP49	Nested P2WPKH	`m/49'/1'/0'`
BIP84	P2WPKH	`m/84'/0'/0'`
BIP86	P2TR Single-key	`m/86'/0'/0'`

The second solution is to back up the path information with the recovery code, making it clear which path is used with which scripts. We call this explicit paths.

The advantage of implicit paths is that users don’t need to keep a record of what paths they use. If the user enters their recovery code into the same wallet application they previously used, of the same version or higher, it will automatically regenerate keys for the same paths it previously used.

The disadvantage of implicit scripts is their inflexibility. When a recovery code is entered, a wallet application must generate the keys for every path it supports and it must scan the blockchain for transactions involving those keys, otherwise it might not find all of a user’s transactions. This is wasteful in wallets that support many features each with their own path if the user only tried a few of those features.

For implicit path recovery codes that don’t include a version number, such as BIP39 and SLIP39, a new version of a wallet application that drops support for an older path can’t warn users during the restore process that some of their funds may not be found. The same problem happens in reverse if a user enters their recovery code into older software: it won’t find newer paths to which the user may have received funds. Recovery codes that include version information, such as Electrum v2 and Aezeed, can detect that a user is entering an older or newer recovery code and direct them to appropriate resources.

The final consequence of implicit paths is that they can only include information that is either universal (such as a standardized path) or derived from the seed (such as keys). Important nondeterministic information that’s specific to a certain user can’t be restored using a recovery code. For example, Alice, Bob, and Carol receive funds that can only be spent with signatures from two out of three of them. Although Alice only needs either Bob’s or Carol’s signature to spend, she needs both of their public keys in order to find their joint funds on the blockchain. That means each of them must back up the public keys for all three of them. As multisignature and other advanced scripts become more common on Bitcoin, the inflexibility of implicit paths becomes more significant.

The advantage of explicit paths is that they can describe exactly what keys should be used with what scripts. There’s no need to support outdated scripts, no problems with backward or forward compatibility, and any extra information (like the public keys of other users) can be included directly. Their disadvantage is that they require users to back up additional information along with their recovery code. The additional information usually can’t compromise a user’s security, so it doesn’t require as much protection as the recovery code, although it can reduce their privacy and does require some protection.

Almost all wallet applications that use explicit paths as of this writing use the output script descriptors standard (called descriptors for short) as specified in BIPs 380, 381, 382, 383, 384, 385, 386, and 389. Descriptors describe a script and the keys (or key paths) to be used with it. A few example descriptors are shown in [sample_descriptors].

Sample descriptors from Bitcoin Core documentation (with elision)
Descriptor	Explanation
`pkh(02c6…9ee5)`	P2PKH script for the provided public key
`sh(multi(2,022f…2a01,03ac…ccbe))`	P2SH multisignature requiring two signatures corresponding to these two keys
`pkh([d34db33f/44'/0'/0']xpub6ERA…RcEL/1/*)`	P2PKH scripts for the BIP32 `d34db33f` with the extended public key (xpub) at the path `M/44'/0'/0'`, which is `xpub6ERA…RcEL`, using the keys at `M/1/*` of that xpub

It has long been the trend for wallet applications designed only for single signature scripts to use implicit paths. Wallet applications designed for multiple signatures or other advanced scripts are increasingly adopting support for explicit paths using descriptors. Applications that do both will usually conform to the standards for implicit paths and also provide descriptors.

A Wallet Technology Stack in Detail

Developers of modern wallets can choose from a variety of different technologies to help users create and use backups—and new solutions appear every year. Instead of going into detail about each of the options we described earlier in this chapter, we’ll focus the rest of this chapter on the stack of technologies we think is most widely used in wallets as of early 2023:

BIP39 recovery codes
BIP32 HD key derivation
BIP44-style implicit paths

All of these standards have been around since 2014 or earlier, and you’ll have no problem finding additional resources for using them. However, if you’re feeling bold, we do encourage you to investigate more modern standards that may provide additional features or safety.

BIP39 Recovery Codes

BIP39 recovery codes are word sequences that represent (encode) a random number used as a seed to derive a deterministic wallet. The sequence of words is sufficient to re-create the seed and from there, re-create all the derived keys. A wallet application that implements deterministic wallets with a BIP39 recovery code will show the user a sequence of 12 to 24 words when first creating a wallet. That sequence of words is the wallet backup and can be used to recover and re-create all the keys in the same or any compatible wallet application. Recovery codes make it easier for users to back up because they are easy to read and correctly transcribe.

Tip

Recovery codes are often confused with "brainwallets." They are not the same. The primary difference is that a brainwallet consists of words chosen by the user, whereas recovery codes are created randomly by the wallet and presented to the user. This important difference makes recovery codes much more secure because humans are very poor sources of randomness.

Note that BIP39 is one implementation of a recovery code standard. BIP39 was proposed by the company behind the Trezor hardware wallet and is compatible with many other wallets applications, although certainly not all.

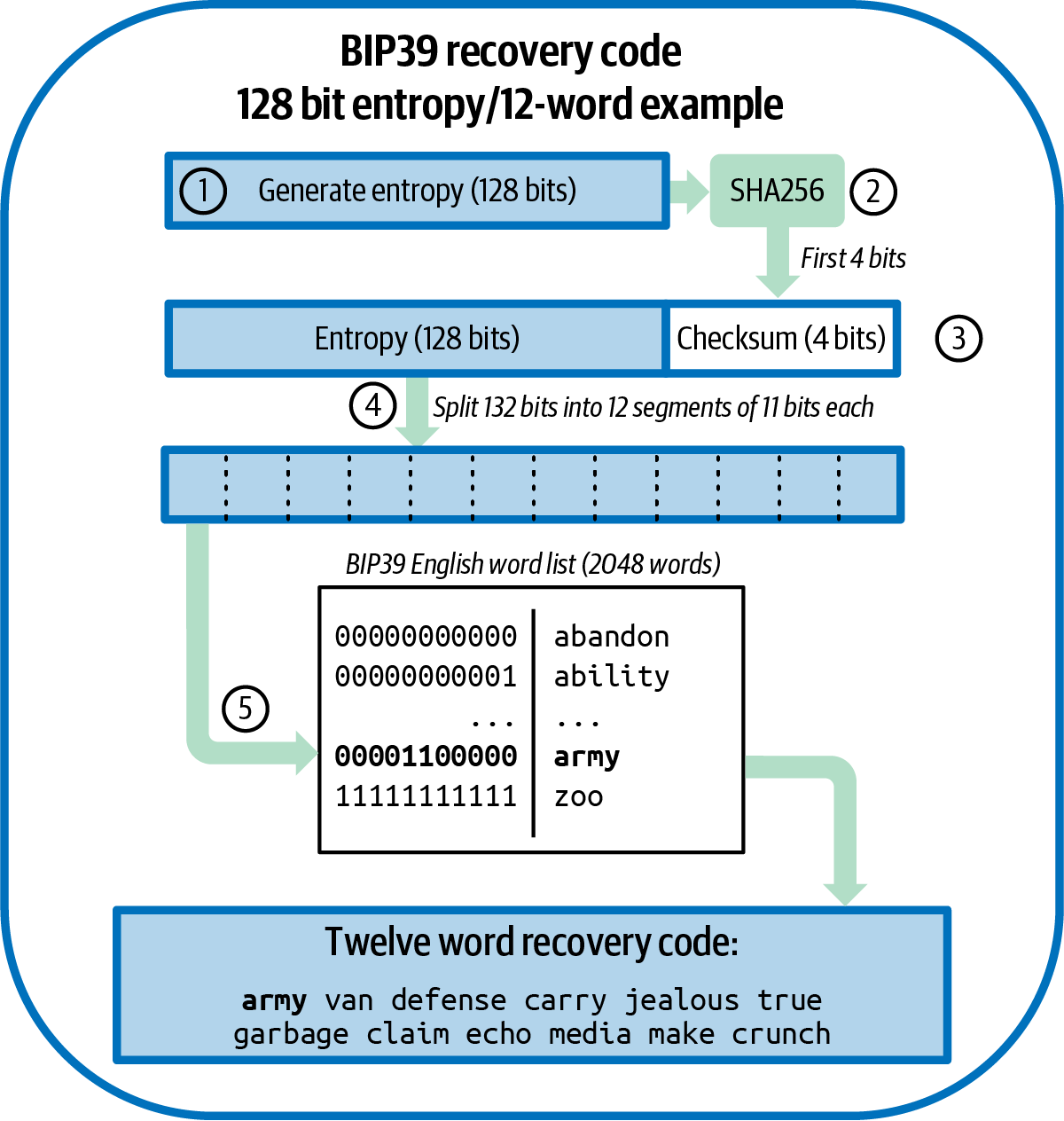
BIP39 defines the creation of a recovery code and seed, which we describe here in nine steps. For clarity, the process is split into two parts: steps 1 through 6 are shown in Generating a recovery code and steps 7 through 9 are shown in From recovery code to seed.

Generating a recovery code

Recovery codes are generated automatically by the wallet application using the standardized process defined in BIP39. The wallet starts from a source of entropy, adds a checksum, and then maps the entropy to a word list:

Create a random sequence (entropy) of 128 to 256 bits.
Create a checksum of the random sequence by taking the first (entropy-length/32) bits of its SHA256 hash.
Add the checksum to the end of the random sequence.
Split the result into 11-bit length segments.
Map each 11-bit value to a word from the predefined dictionary of 2,048 words.
The recovery code is the sequence of words.

Generating entropy and encoding as a recovery code. shows how entropy is used to generate a BIP39 recovery code.

Figure 4. Generating entropy and encoding as a recovery code.

[table_4-5] shows the relationship between the size of the entropy data and the length of recovery code in words.

BIP39: entropy and word length
Entropy (bits)	Checksum (bits)	Entropy + checksum (bits)	Recovery code words
128	4	132	12
160	5	165	15
192	6	198	18
224	7	231	21
256	8	264	24

From recovery code to seed

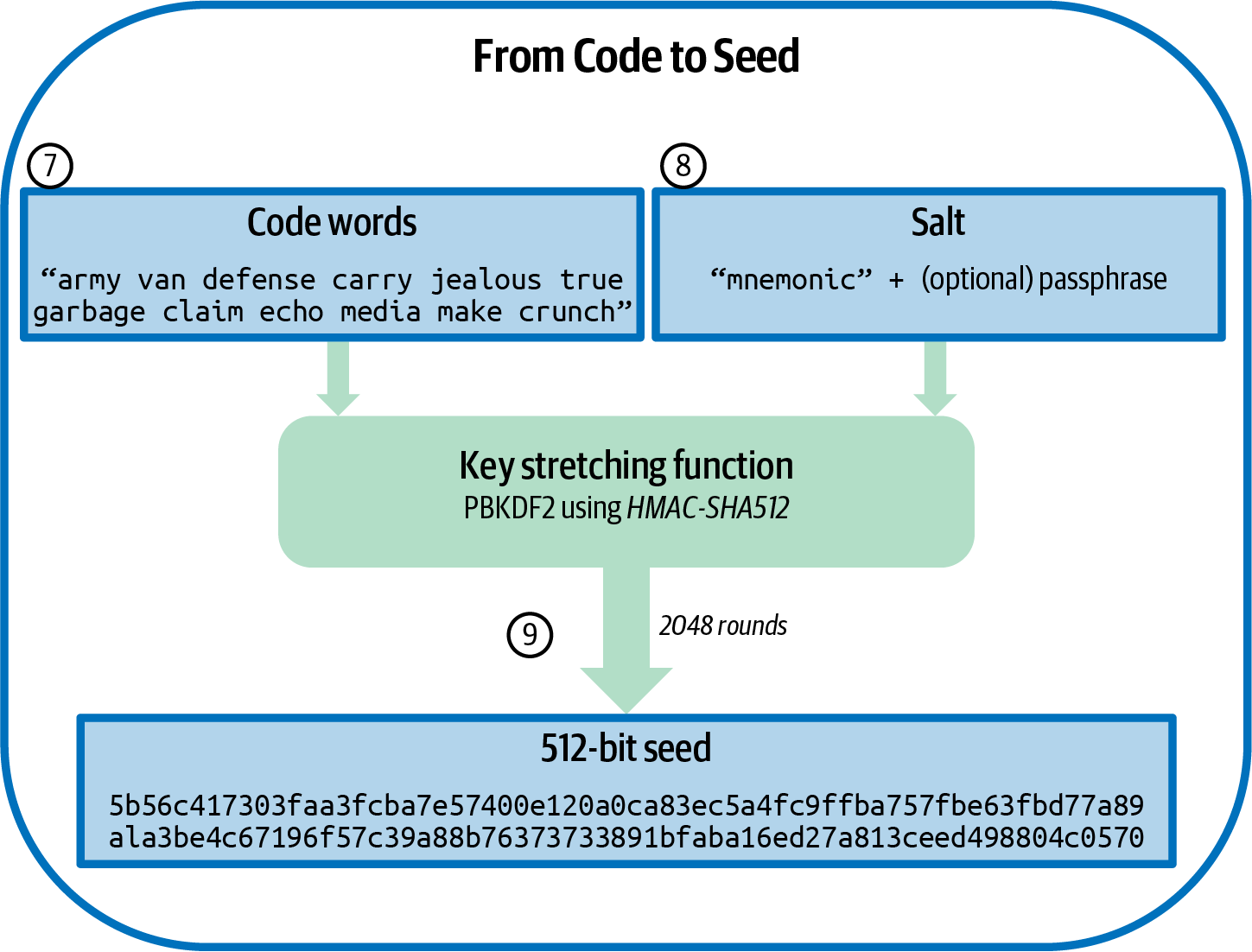
The recovery code represents entropy with a length of 128 to 256 bits. The entropy is then used to derive a longer (512-bit) seed through the use of the key-stretching function PBKDF2. The seed produced is then used to build a deterministic wallet and derive its keys.

The key-stretching function takes two parameters: the entropy and a salt. The purpose of a salt in a key-stretching function is to make it difficult to build a lookup table enabling a brute-force attack. In the BIP39 standard, the salt has another purpose—it allows the introduction of a passphrase that serves as an additional security factor protecting the seed, as we will describe in more detail in Optional passphrase in BIP39.

Tip

The key-stretching function, with its 2,048 rounds of hashing, makes it slightly harder to brute-force attack the recovery code using software. Special-purpose hardware is not significantly affected. For an attacker who needs to guess a user’s entire recovery code, the length of the code (128 bits at a minimum) provides more than sufficient security. But for cases where an attacker might learn a small part of the user’s code, key-stretching adds some security by slowing down how fast an attacker can check different recovery code combinations. BIP39’s parameters were considered weak by modern standards even when it was first published almost a decade ago, although that’s likely a consequence of being designed for compatibility with hardware signing devices with low-powered CPUs. Some alternatives to BIP39 use stronger key-stretching parameters, such as Aezeed’s 32,768 rounds of hashing using the more complex Scrypt algorithm, although they may not be as convenient to run on hardware signing devices.

The process described in steps 7 through 9 continues from the process described previously in Generating a recovery code:

The first parameter to the PBKDF2 key-stretching function is the entropy produced from step 6.
The second parameter to the PBKDF2 key-stretching function is a salt. The salt is composed of the string constant "mnemonic" concatenated with an optional user-supplied passphrase string.
PBKDF2 stretches the recovery code and salt parameters using 2,048 rounds of hashing with the HMAC-SHA512 algorithm, producing a 512-bit value as its final output. That 512-bit value is the seed.

From recovery code to seed. shows how a recovery code is used to generate a seed.

Figure 5. From recovery code to seed.

Tables #bip39_128_no_pass, #bip39_128_w_pass, and #bip39_256_no_pass show some examples of recovery codes and the seeds they produce.

128-bit entropy BIP39 recovery code, no passphrase, resulting seed
Entropy input (128 bits)	`0c1e24e5917779d297e14d45f14e1a1a`
Recovery Code (12 words)	`army van defense carry jealous true garbage claim echo media make crunch`
Passphrase	(none)
Seed (512 bits)	`5b56c417303faa3fcba7e57400e120a0ca83ec5a4fc9ffba757fbe63fbd77a89a1a3be4` `c67196f57c39a88b76373733891bfaba16ed27a813ceed498804c0570`

128-bit entropy BIP39 recovery code, with passphrase, resulting seed
Entropy input (128 bits)	`0c1e24e5917779d297e14d45f14e1a1a`
Recovery Code (12 words)	`army van defense carry jealous true garbage claim echo media make crunch`
Passphrase	SuperDuperSecret
Seed (512 bits)	`3b5df16df2157104cfdd22830162a5e170c0161653e3afe6c88defeefb0818c793dbb28` `ab3ab091897d0715861dc8a18358f80b79d49acf64142ae57037d1d54`

256-bit entropy BIP39 recovery code, no passphrase, resulting seed
Entropy input (256 bits)	`2041546864449caff939d32d574753fe684d3c947c3346713dd8423e74abcf8c`
Recovery Code (24 words)	`cake apple borrow silk endorse fitness top denial coil riot stay wolf luggage oxygen faint major edit measure invite love trap field dilemma oblige`
Passphrase	(none)
Seed (512 bits)	`3269bce2674acbd188d4f120072b13b088a0ecf87c6e4cae41657a0bb78f5315b33b3` `a04356e53d062e55f1e0deaa082df8d487381379df848a6ad7e98798404`

How Much Entropy Do You Need?

BIP32 allows seeds to be from 128 to 512 bits. BIP39 accepts from 128 to 256 bits of entropy; Electrum v2 accepts 132 bits of entropy; Aezeed accepts 128 bits of entropy; SLIP39 accepts either 128 or 256 bits. The variation in these numbers makes it unclear how much entropy is needed for safety. We’ll try to demystify that.

BIP32 extended private keys consist of a 256-bit key and a 256-bit chain code, for a total of 512 bits. That means there’s a maximum of 2⁵¹² different possible extended private keys. If you start with more than 512 bits of entropy, you’ll still get an extended private key containing 512 bits of entropy—so there’s no point in using more than 512 bits even if any of the standards we mentioned allowed that.

However, even though there are 2⁵¹² different extended private keys, there are only (slightly less than) 2²⁵⁶ regular private keys—and its those private keys that actually secure your bitcoins. That means, if you use more than 256 bits of entropy for your seed, you still get private keys containing only 256 bits of entropy. There may be future Bitcoin-related protocols where extra entropy in the extended keys provides extra security, but that’s not currently the case.

The security strength of a Bitcoin public key is 128 bits. An attacker with a classical computer (the only kind which can be used for a practical attack as of this writing) would need to perform about 2¹²⁸ operations on Bitcoin’s elliptic curve in order to find a private key for another user’s public key. The implication of a security strength of 128 bits is that there’s no apparent benefit to using more than 128 bits of entropy (although you need to ensure your generated private keys are selected uniformly from within the entire 2²⁵⁶ range of private keys).

There is one extra benefit of greater entropy: if a fixed percentage of your recovery code (but not the whole code) is seen by an attacker, the greater the entropy, the harder it will be for them to figure out part of the code they didn’t see. For example, if an attacker sees half of a 128-bit code (64 bits), it’s plausible that they’ll be able to brute force the remaining 64 bits. If they see half of a 256-bit code (128 bits), it’s not plausible that they can brute force the other half. We don’t recommend relying on this defense—either keep your recovery codes very safe or use a method like SLIP39 that lets you distribute your recovery code across multiple locations without relying on the safety of any individual code.

As of 2023, most modern wallets generate 128 bits of entropy for their recovery codes (or a value near 128, such as Electrum v2’s 132 bits).

Optional passphrase in BIP39

The BIP39 standard allows the use of an optional passphrase in the derivation of the seed. If no passphrase is used, the recovery code is stretched with a salt consisting of the constant string "mnemonic", producing a specific 512-bit seed from any given recovery code. If a passphrase is used, the stretching function produces a different seed from that same recovery code. In fact, given a single recovery code, every possible passphrase leads to a different seed. Essentially, there is no "wrong" passphrase. All passphrases are valid and they all lead to different seeds, forming a vast set of possible uninitialized wallets. The set of possible wallets is so large (2⁵¹²) that there is no practical possibility of brute-forcing or accidentally guessing one that is in use.

Tip	There are no "wrong" passphrases in BIP39. Every passphrase leads to some wallet, which unless previously used will be empty.

The optional passphrase creates two important features:

A second factor (something memorized) that makes a recovery code useless on its own, protecting recovery codes from compromise by a casual thief. For protection from a tech-savvy thief, you will need to use a very strong passphrase.
A form of plausible deniability or "duress wallet," where a chosen passphrase leads to a wallet with a small amount of funds used to distract an attacker from the "real" wallet that contains the majority of funds.

It’s important to note that the use of a passphrase also introduces the risk of loss:

If the wallet owner is incapacitated or dead and no one else knows the passphrase, the seed is useless and all the funds stored in the wallet are lost forever.
Conversely, if the owner backs up the passphrase in the same place as the seed, it defeats the purpose of a second factor.

While passphrases are very useful, they should only be used in combination with a carefully planned process for backup and recovery, considering the possibility of surviving the owner and allowing his or her family to recover the cryptocurrency estate.

Creating an HD Wallet from the Seed

HD wallets are created from a single root seed, which is a 128-, 256-, or 512-bit random number. Most commonly, this seed is generated by or decrypted from a recovery code as detailed in the previous section.

Every key in the HD wallet is deterministically derived from this root seed, which makes it possible to re-create the entire HD wallet from that seed in any compatible HD wallet. This makes it easy to back up, restore, export, and import HD wallets containing thousands or even millions of keys by simply transferring only the recovery code that the root seed is derived from. The process of creating the master keys and master chain code for an HD wallet is shown in Creating master keys and chain code from a root seed..

Figure 6. Creating master keys and chain code from a root seed.

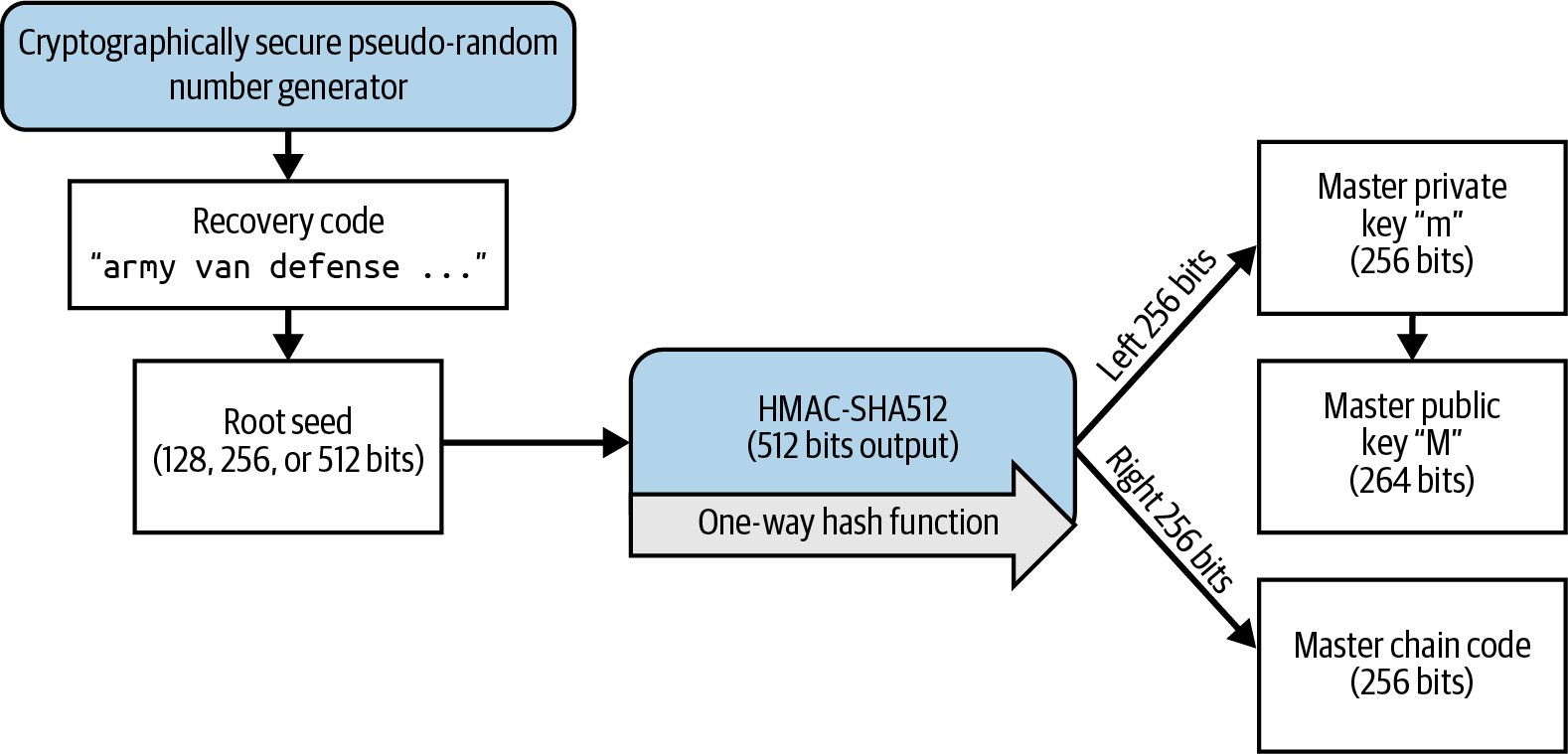
The root seed is input into the HMAC-SHA512 algorithm and the resulting hash is used to create a master private key (m) and a master chain code (c).

The master private key (m) then generates a corresponding master public key (M) using the normal elliptic curve multiplication process m × G that we saw in [public_key_derivation].

The master chain code (c) is used to introduce entropy in the function that creates child keys from parent keys, as we will see in the next section.

Private child key derivation

HD wallets use a child key derivation (CKD) function to derive child keys from parent keys.

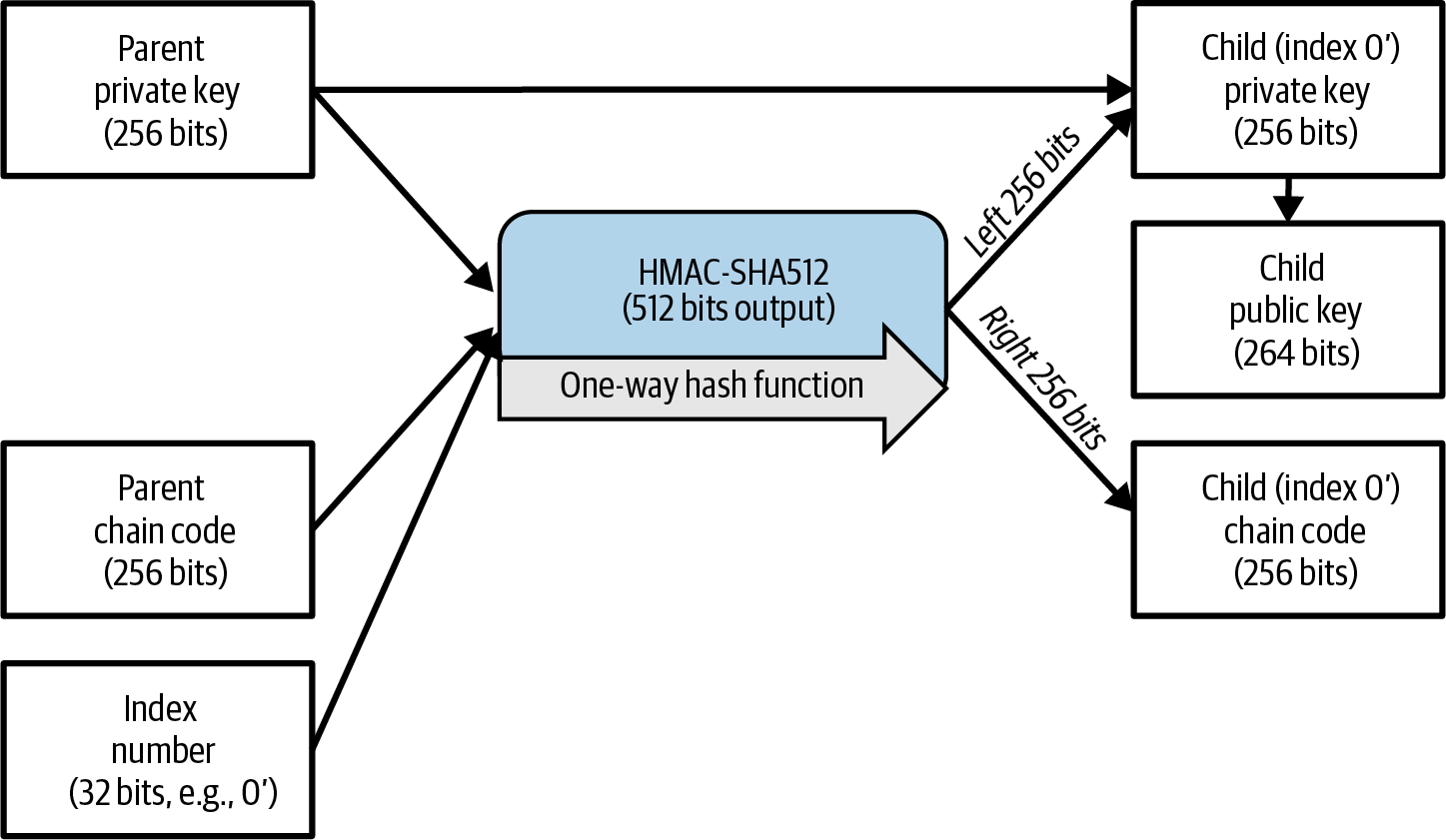
The child key derivation functions are based on a one-way hash function that combines:

A parent private or public key (uncompressed key)
A seed called a chain code (256 bits)
An index number (32 bits)

The chain code is used to introduce deterministic random data to the process, so that knowing the index and a child key is not sufficient to derive other child keys. Knowing a child key does not make it possible to find its siblings unless you also have the chain code. The initial chain code seed (at the root of the tree) is made from the seed, while subsequent child chain codes are derived from each parent chain code.

These three items (parent key, chain code, and index) are combined and hashed to generate children keys, as follows.

The parent public key, chain code, and the index number are combined and hashed with the HMAC-SHA512 algorithm to produce a 512-bit hash. This 512-bit hash is split into two 256-bit halves. The right-half 256 bits of the hash output become the chain code for the child. The left-half 256 bits of the hash are added to the parent private key to produce the child private key. In Extending a parent private key to create a child private key., we see this illustrated with the index set to 0 to produce the "zero" (first by index) child of the parent.

Figure 7. Extending a parent private key to create a child private key.

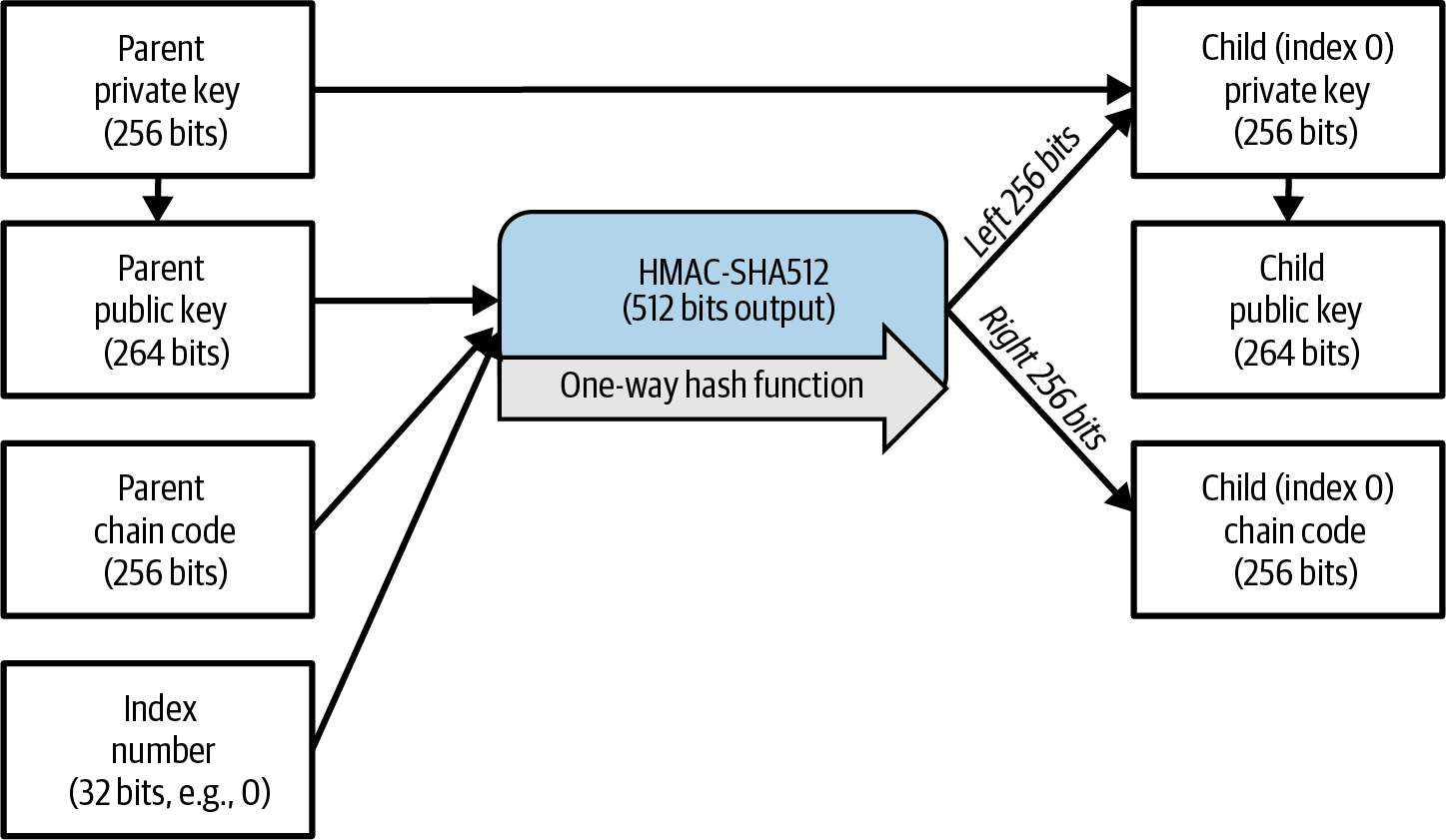
Changing the index allows us to extend the parent and create the other children in the sequence (e.g., Child 0, Child 1, Child 2, etc.). Each parent key can have 2,147,483,647 (2³¹) children (2³¹ is half of the entire 2³² range available because the other half is reserved for a special type of derivation we will talk about later in this chapter).

Repeating the process one level down the tree, each child can in turn become a parent and create its own children, in an infinite number of generations.

Using derived child keys

Child private keys are indistinguishable from nondeterministic (random) keys. Because the derivation function is a one-way function, the child key cannot be used to find the parent key. The child key also cannot be used to find any siblings. If you have the n^th child, you cannot find its siblings, such as the n–1 child or the n+1 child, or any other children that are part of the sequence. Only the parent key and chain code can derive all the children. Without the child chain code, the child key cannot be used to derive any grandchildren either. You need both the child private key and the child chain code to start a new branch and derive grandchildren.

So what can the child private key be used for on its own? It can be used to make a public key and a Bitcoin address. Then, it can be used to sign transactions to spend anything paid to that address.

Tip

A child private key, the corresponding public key, and the Bitcoin address are all indistinguishable from keys and addresses created randomly. The fact that they are part of a sequence is not visible outside of the HD wallet function that created them. Once created, they operate exactly as "normal" keys.

Extended keys

As we saw earlier, the key derivation function can be used to create children at any level of the tree, based on the three inputs: a key, a chain code, and the index of the desired child. The two essential ingredients are the key and chain code, and combined these are called an extended key. The term "extended key" could also be thought of as "extensible key" because such a key can be used to derive children.

Extended keys are stored and represented simply as the concatenation of the key and chain code. There are two types of extended keys. An extended private key is the combination of a private key and chain code and can be used to derive child private keys (and from them, child public keys). An extended public key is a public key and chain code, which can be used to create child public keys (public only), as described in [public_key_derivation].

Think of an extended key as the root of a branch in the tree structure of the HD wallet. With the root of the branch, you can derive the rest of the branch. The extended private key can create a complete branch, whereas the extended public key can only create a branch of public keys.

Extended keys are encoded using base58check, to easily export and import between different BIP32-compatible wallets. The base58check coding for extended keys uses a special version number that results in the prefix "xprv" and "xpub" when encoded in base58 characters to make them easily recognizable. Because the extended key contains many more bytes than regular addresses, it is also much longer than other base58check-encoded strings we have seen previously.

Here’s an example of an extended private key, encoded in base58check:

xprv9tyUQV64JT5qs3RSTJkXCWKMyUgoQp7F3hA1xzG6ZGu6u6Q9VMNjGr67Lctvy5P8oyaYAL9CA
WrUE9i6GoNMKUga5biW6Hx4tws2six3b9c

Here’s the corresponding extended public key, encoded in base58check:

xpub67xpozcx8pe95XVuZLHXZeG6XWXHpGq6Qv5cmNfi7cS5mtjJ2tgypeQbBs2UAR6KECeeMVKZBP
LrtJunSDMstweyLXhRgPxdp14sk9tJPW9

Public child key derivation

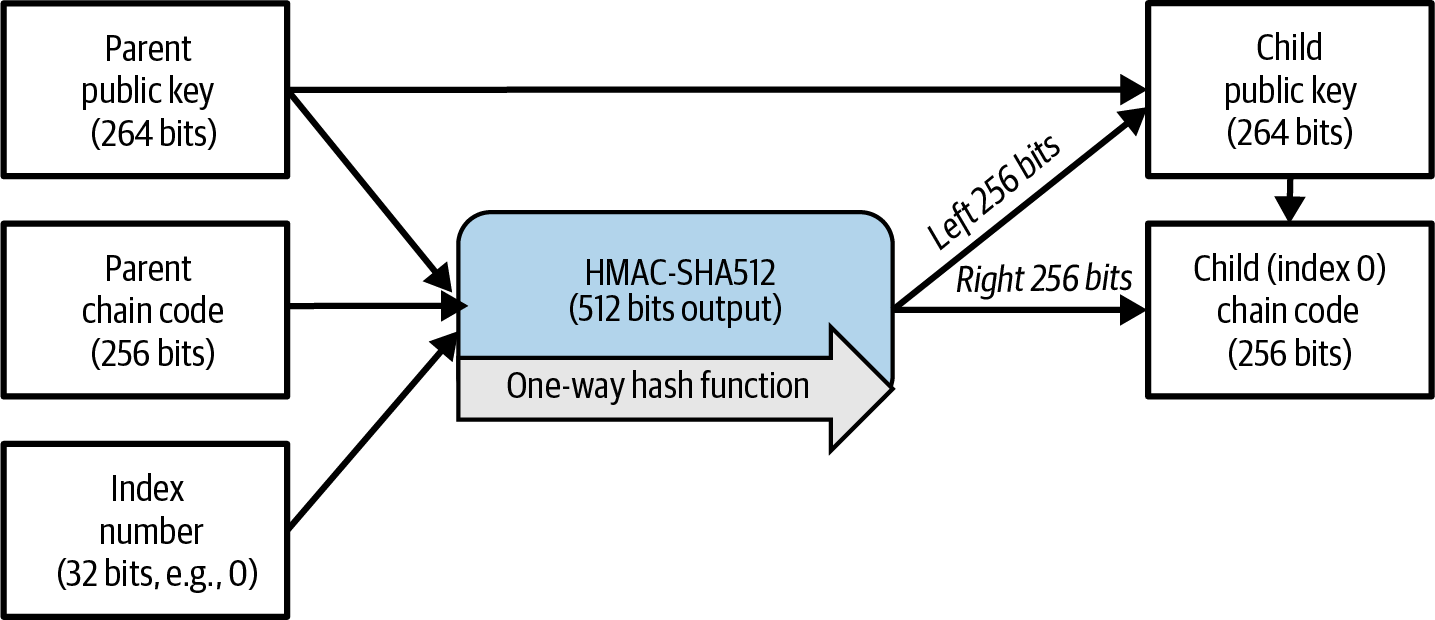
As mentioned previously, a very useful characteristic of HD wallets is the ability to derive public child keys from public parent keys without having the private keys. This gives us two ways to derive a child public key: either from the child private key or directly from the parent public key.

An extended public key can be used, therefore, to derive all of the public keys (and only the public keys) in that branch of the HD wallet structure.

This shortcut can be used to create public key–only deployments where a server or application has a copy of an extended public key and no private keys whatsoever. That kind of deployment can produce an infinite number of public keys and Bitcoin addresses but cannot spend any of the money sent to those addresses. Meanwhile, on another, more secure server, the extended private key can derive all the corresponding private keys to sign transactions and spend the money.

One common application of this solution is to install an extended public key on a web server that serves an ecommerce application. The web server can use the public key derivation function to create a new Bitcoin address for every transaction (e.g., for a customer shopping cart). The web server will not have any private keys that would be vulnerable to theft. Without HD wallets, the only way to do this is to generate thousands of Bitcoin addresses on a separate secure server and then preload them on the ecommerce server. That approach is cumbersome and requires constant maintenance to ensure that the ecommerce server doesn’t "run out" of keys.

Mind the Gap

An extended public key can generate approximately 4 billion direct child keys, far more than any store or application should ever need. However, it would also take a wallet application an unreasonable amount of time to generate all 4 billion keys and scan the blockchain for transactions involving those keys. For that reason, most wallets only generate a few keys at a time, scan for payments involving those keys, and generate additional keys in the sequence as the previous keys are used. For example, Alice’s wallet generates 100 keys. When it sees a payment to the first key, it generates the 101st key.

Sometimes a wallet application will distribute a key to someone who later decides not to pay, creating a gap in the key chain. That’s fine as long as the wallet has already generated keys after the gap so that it finds later payments and continues generating more keys. The maximum number of unused keys in a row that can fail to receive a payment without causing problems is called the gap limit.

When a wallet application has distributed all of the keys up to its gap limit and none of those keys have received a payment, it has three options about how to handle future requests for new keys:

It can refuse the requests, preventing it from receiving any further payments. This is obviously an unpalatable option, although it’s the simplest to implement.
It can generate new keys beyond its gap limit. This ensures that every person requesting to pay gets a unique key, preventing address reuse and improving privacy. However, if the wallet needs to be restored from a recovery code, or if the wallet owner is using other software loaded with the same extended public key, those other wallets won’t see any payments received after the extended gap.
It can distribute keys it previously distributed, ensuring a smooth recovery but potentially reducing the privacy of the wallet owner and the people with whom they transact.

Open source production systems for online merchants, such as BTCPay Server, attempt to dodge this problem by using very large gap limits and limiting the rate at which they generate invoices. Other solutions have been proposed, such as asking the spender’s wallet to construct (but not broadcast) a transaction paying a possibly reused address before they receive a fresh address for the actual transaction. However, these other solutions have not been used in production as of this writing.

Another common application of this solution is for cold-storage or hardware signing devices. In that scenario, the extended private key can be stored on a paper wallet or hardware device, while the extended public key can be kept online. The user can create "receive" addresses at will, while the private keys are safely stored offline. To spend the funds, the user can use the extended private key on an offline software wallet application or the hardware signing device. Extending a parent public key to create a child public key. illustrates the mechanism for extending a parent public key to derive child public keys.

Figure 8. Extending a parent public key to create a child public key.

Using an Extended Public Key on a Web Store

Let’s see how HD wallets are used by looking at Gabriel’s web store.

Gabriel first set up his web store as a hobby, based on a simple hosted WordPress page. His store was quite basic with only a few pages and an order form with a single Bitcoin address.

Gabriel used the first Bitcoin address generated by his regular wallet as the main Bitcoin address for his store. Customers would submit an order using the form and send payment to Gabriel’s published Bitcoin address, triggering an email with the order details for Gabriel to process. With just a few orders each week, this system worked well enough, even though it weakened the privacy of Gabriel, his clients, and the people he paid.

However, the little web store became quite successful and attracted many orders from the local community. Soon, Gabriel was overwhelmed. With all the orders paying the same address, it became difficult to correctly match orders and transactions, especially when multiple orders for the same amount came in close together.

The only metadata that is chosen by the receiver of a typical Bitcoin transaction are the amount and payment address. There’s no subject or message field that can be used to hold a unique identifier invoice number.

Gabriel’s HD wallet offers a much better solution through the ability to derive public child keys without knowing the private keys. Gabriel can load an extended public key (xpub) on his website, which can be used to derive a unique address for every customer order. The unique address immediately improves privacy and also gives each order a unique identifier that can be used for tracking which invoices have been paid.

Using the HD wallet allows Gabriel to spend the funds from his personal wallet application, but the xpub loaded on the website can only generate addresses and receive funds. This feature of HD wallets is a great security feature. Gabriel’s website does not contain any private keys and therefore any hack of it can only steal the funds Gabriel would have received in the future, not any funds he received in the past.

To export the xpub from his Trezor hardware signing device, Gabriel uses the web-based Trezor wallet application. The Trezor device must be plugged in for the public keys to be exported. Note that most hardware signing devices will never export private keys—those always remain on the device.

Gabriel copies the xpub to his web store’s Bitcoin payment processing software, such as the widely used open source BTCPay Server.

Hardened child key derivation

The ability to derive a branch of public keys from an xpub is very useful, but it comes with a potential risk. Access to an xpub does not give access to child private keys. However, because the xpub contains the chain code, if a child private key is known, or somehow leaked, it can be used with the chain code to derive all the other child private keys. A single leaked child private key, together with a parent chain code, reveals all the private keys of all the children. Worse, the child private key together with a parent chain code can be used to deduce the parent private key.

To counter this risk, HD wallets provide an alternative derivation function called hardened derivation, which breaks the relationship between parent public key and child chain code. The hardened derivation function uses the parent private key to derive the child chain code, instead of the parent public key. This creates a "firewall" in the parent/child sequence, with a chain code that cannot be used to compromise a parent or sibling private key. The hardened derivation function looks almost identical to the normal child private key derivation, except that the parent private key is used as input to the hash function, instead of the parent public key, as shown in the diagram in Hardened derivation of a child key; omits the parent public key..

Figure 9. Hardened derivation of a child key; omits the parent public key.

When the hardened private derivation function is used, the resulting child private key and chain code are completely different from what would result from the normal derivation function. The resulting "branch" of keys can be used to produce extended public keys that are not vulnerable because the chain code they contain cannot be exploited to reveal any private keys for their siblings or parents. Hardened derivation is therefore used to create a "gap" in the tree above the level where extended public keys are used.

In simple terms, if you want to use the convenience of an xpub to derive branches of public keys, without exposing yourself to the risk of a leaked chain code, you should derive it from a hardened parent rather than a normal parent. As a best practice, the level-1 children of the master keys are always derived through the hardened derivation to prevent compromise of the master keys.

Index numbers for normal and hardened derivation

The index number used in the derivation function is a 32-bit integer. To easily distinguish between keys created through the normal derivation function versus keys derived through hardened derivation, this index number is split into two ranges. Index numbers between 0 and 2³¹ – 1 (0x0 to 0x7FFFFFFF) are used only for normal derivation. Index numbers between 2³¹ and 2³² – 1 (0x80000000 to 0xFFFFFFFF) are used only for hardened derivation. Therefore, if the index number is less than 2³¹, the child is normal, whereas if the index number is equal or above 2³¹, the child is hardened.

To make the index number easier to read and display, the index number for hardened children is displayed starting from zero, but with a prime symbol. The first normal child key is therefore displayed as 0, whereas the first hardened child (index 0x80000000) is displayed as 0'. In a sequence then, the second hardened key would have index 0x80000001 and would be displayed as 1', and so on. When you see an HD wallet index i', that means 2³¹+i. In regular ASCII text, the prime symbol is substituted with either a single apostrophe or the letter h. For situations, such as in output script descriptors, where text may be used in a shell or other context where a single apostrophe has special meaning, using the letter h is recommended.

HD wallet key identifier (path)

Keys in an HD wallet are identified using a "path" naming convention, with each level of the tree separated by a slash (/) character (see [table_4-8]). Private keys derived from the master private key start with "m." Public keys derived from the master public key start with "M." Therefore, the first child private key of the master private key is m/0. The first child public key is M/0. The second grandchild of the first child is m/0/1, and so on.

The "ancestry" of a key is read from right to left, until you reach the master key from which it was derived. For example, identifier m/x/y/z describes the key that is the z-th child of key m/x/y, which is the y-th child of key m/x, which is the x-th child of m.

HD wallet path examples
HD path	Key described
m/0	The first (0) child private key from the master private key (m)
m/0/0	The first grandchild private key from the first child (m/0)
m/0'/0	The first normal grandchild private key from the first hardened child (m/0')
m/1/0	The first grandchild private key from the second child (m/1)
M/23/17/0/0	The first great-great-grandchild public key from the first great-grandchild from the 18th grandchild from the 24th child

Navigating the HD wallet tree structure

The HD wallet tree structure offers tremendous flexibility. Each parent extended key can have 4 billion children: 2 billion normal children and 2 billion hardened children. Each of those children can have another 4 billion children, and so on. The tree can be as deep as you want, with an infinite number of generations. With all that flexibility, however, it becomes quite difficult to navigate this infinite tree. It is especially difficult to transfer HD wallets between implementations because the possibilities for internal organization into branches and subbranches are endless.

Two BIPs offer a solution to this complexity by creating some proposed standards for the structure of HD wallet trees. BIP43 proposes the use of the first hardened child index as a special identifier that signifies the "purpose" of the tree structure. Based on BIP43, an HD wallet should use only one level-1 branch of the tree, with the index number identifying the structure and namespace of the rest of the tree by defining its purpose. For example, an HD wallet using only branch m/i'/ is intended to signify a specific purpose, and that purpose is identified by index number "i."

Extending that specification, BIP44 proposes a multiaccount structure as "purpose" number 44' under BIP43. All HD wallets following the BIP44 structure are identified by the fact that they only used one branch of the tree: m/44'/.

BIP44 specifies the structure as consisting of five predefined tree levels:

m / purpose' / coin_type' / account' / change / address_index

The first-level "purpose" is always set to 44'. The second-level "coin_type" specifies the type of cryptocurrency coin, allowing for multicurrency HD wallets where each currency has its own subtree under the second level. Bitcoin is m/44'/0' and Bitcoin Testnet is m/44'/1'.

The third level of the tree is "account," which allows users to subdivide their wallets into separate logical subaccounts for accounting or organizational purposes. For example, an HD wallet might contain two Bitcoin "accounts": m/44'/0'/0' and m/44'/0'/1'. Each account is the root of its own subtree.

On the fourth level, "change," an HD wallet has two subtrees, one for creating receiving addresses and one for creating change addresses. Note that whereas the previous levels used hardened derivation, this level uses normal derivation. This is to allow this level of the tree to export extended public keys for use in a nonsecured environment. Usable addresses are derived by the HD wallet as children of the fourth level, making the fifth level of the tree the "address_index." For example, the third receiving address for payments in the primary account would be M/44'/0'/0'/0/2. [table_4-9] shows a few more examples.

BIP44 HD wallet structure examples
HD path	Key described
M/44`'`/0`'`/0`'`/0/2	The third receiving public key for the primary Bitcoin account
M/44`'`/0`'`/3`'`/1/14	The fifteenth change-address public key for the fourth Bitcoin account
m/44`'`/2`'`/0`'`/0/1	The second private key in the Litecoin main account, for signing transactions

Many people focus on securing their bitcoins against theft and other attacks, but one of the leading causes of lost bitcoins—perhaps the leading cause—is data loss. If the keys and other essential data required to spend your bitcoins is lost, those bitcoins will forever be unspendable. Nobody can get them back for you. In this chapter, we looked at the systems that modern wallet applications use to help you prevent losing that data. Remember, however, that it’s up to you to actually use the systems available to make good backups and regularly test them.