Mining and Consensus
The word "mining" is somewhat misleading. By evoking the extraction of precious metals, it focuses our attention on the reward for mining, the new bitcoins created in each block. Although mining is incentivized by this reward, the primary purpose of mining is not the reward or the generation of new bitcoins. If you view mining only as the process by which bitcoins are created, you are mistaking the means (incentives) as the goal of the process. Mining is the mechanism that underpins the decentralized clearinghouse, by which transactions are validated and cleared. Mining is one of the inventions that makes Bitcoin special, a decentralized consensus mechanism that is the basis for P2P digital cash.
Mining secures the Bitcoin system and enables the emergence of network-wide consensus without a central authority. The reward of newly minted bitcoins and transaction fees is an incentive scheme that aligns the actions of miners with the security of the network, while simultaneously implementing the monetary supply.
|
Tip
|
Mining is one of the mechanisms by which Bitcoin’s consensus security is decentralized. |
Miners record new transactions on the global blockchain. A new block, containing transactions that occurred since the last block, is mined every 10 minutes on average, thereby adding those transactions to the blockchain. Transactions that become part of a block and added to the blockchain are considered confirmed, which allows the new owners of the bitcoins to know that irrevocable effort was expended securing the bitcoins they received in those transactions.
Additionally, transactions in the blockchain have a topological order defined by their position in the blockchain. One transaction is earlier than another if it appears in an earlier block or if it appears earlier in the same block. In the Bitcoin protocol, a transaction is only valid if it spends the outputs of transactions that appeared earlier in the blockchain (whether they are earlier in the same block or in an earlier block), and only if no previous transaction spent any of those same outputs. Within a single chain of blocks, the enforcement of topological ordering ensures no two valid transactions can spend the same output, eliminating the problem of double spending.
In some protocols built on top of Bitcoin, the topological order of Bitcoin transactions is also used to establish a sequence of events; we’ll discuss that idea further in [single_use_seals].
Miners receive two types of rewards in return for the security provided by mining: new bitcoins created with each new block (called the subsidy), and transaction fees from all the transactions included in the block. To earn this reward, miners compete to satisfy a challenge based on a cryptographic hash algorithm. The solution to the problem, called the proof of work, is included in the new block and acts as proof that the miner expended significant computing effort. The competition to solve the proof-of-work algorithm to earn the reward and the right to record transactions on the blockchain is the basis for Bitcoin’s security model.
Bitcoin’s money supply is created in a process that’s similar to how a central bank issues new money by printing bank notes. The maximum amount of newly created bitcoin a miner can add to a block decreases approximately every four years (or precisely every 210,000 blocks). It started at 50 bitcoins per block in January 2009 and halved to 25 bitcoins per block in November 2012. It halved again to 12.5 bitcoins in July 2016, and again to 6.25 in May 2020. Based on this formula, mining rewards decrease exponentially until approximately the year 2140, when all bitcoins will have been issued. After 2140, no new bitcoin will be issued.
Bitcoin miners also earn fees from transactions. Every transaction may include a transaction fee in the form of a surplus of bitcoins between the transaction’s inputs and outputs. The winning bitcoin miner gets to "keep the change" on the transactions included in the winning block. Today, the fees usually represent only a small percentage of a miner’s income, with the vast majority coming from the newly minted bitcoins. However, as the reward decreases over time and the number of transactions per block increases, a greater proportion of mining earnings will come from fees. Gradually, the mining reward will be dominated by transaction fees, which will form the primary incentive for miners. After 2140, the amount of new bitcoins in each block drops to zero and mining will be incentivized only by transaction fees.
In this chapter, we will first examine mining as a monetary supply mechanism and then look at the most important function of mining: the decentralized consensus mechanism that underpins Bitcoin’s security.
To understand mining and consensus, we will track Alice’s transaction as it is received and added to a block by Jing’s mining equipment. Then we will follow the block as it is mined, added to the blockchain, and accepted by the Bitcoin network through the process of emergent consensus.
Bitcoin Economics and Currency Creation
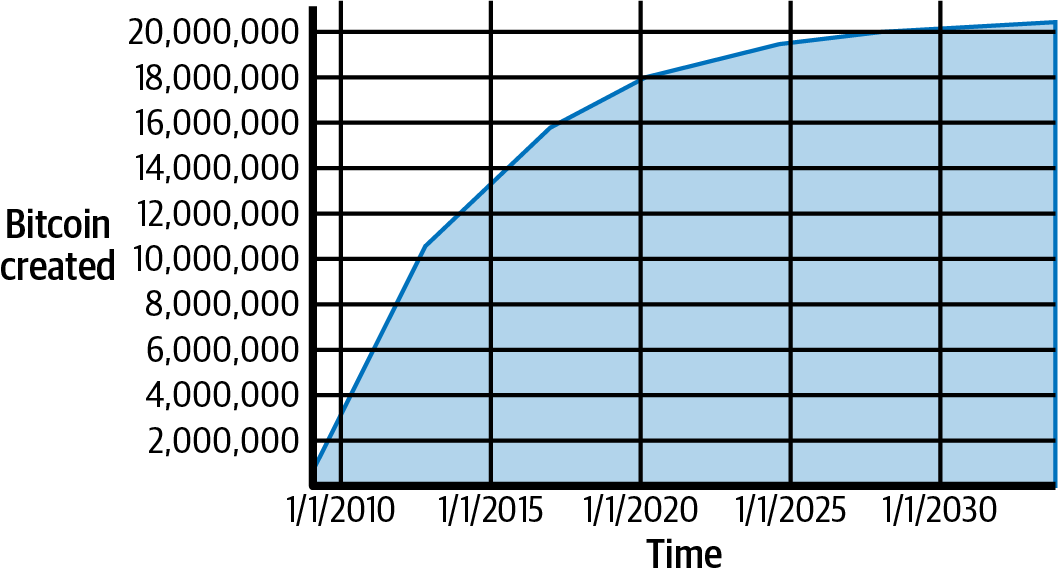
Bitcoin are minted during the creation of each block at a fixed and diminishing rate. Each block, generated on average every 10 minutes, contains entirely new bitcoins, created from nothing. Every 210,000 blocks, or approximately every four years, the currency issuance rate is decreased by 50%. For the first four years of operation of the network, each block contained 50 new bitcoins.
The first halving occurred at block 210,000. The next expected halving after publication of this book will occur at block 840,000, which will probably be produced in April or May of 2024. The rate of new bitcoins decreases exponentially over 32 of these halvings until block 6,720,000 (mined approximately in year 2137), when it reaches the minimum currency unit of 1 satoshi. Finally, after 6.93 million blocks, in approximately 2140, almost 2,099,999,997,690,000 satoshis, or almost 21 million bitcoin, will have been issued. Thereafter, blocks will contain no new bitcoins, and miners will be rewarded solely through the transaction fees. Supply of bitcoin currency over time based on a geometrically decreasing issuance rate. shows the total bitcoins in circulation over time, as the issuance of currency decreases.
|
Note
|
The maximum number of bitcoins mined is the upper limit of possible mining rewards for Bitcoin. In practice, a miner may intentionally mine a block taking less than the full reward. Such blocks have already been mined and more may be mined in the future, resulting in a lower total issuance of the currency. |
In the code in A script for calculating how much total bitcoin will be issued, we calculate the total amount of bitcoin that will be issued.
# Original block reward for miners was 50 BTC
start_block_reward = 50
# 210000 is around every 4 years with a 10 minute block interval
reward_interval = 210000
def max_money():
# 50 BTC = 50 0000 0000 Satoshis
current_reward = 50 * 10**8
total = 0
while current_reward > 0:
total += reward_interval * current_reward
current_reward /= 2
return total
print("Total BTC to ever be created:", max_money(), "Satoshis")Running the max_money.py script shows the output produced by running this script.
$ python max_money.py
Total BTC to ever be created: 2099999997690000 SatoshisThe finite and diminishing issuance creates a fixed monetary supply that resists inflation. Unlike a fiat currency, which can be printed in infinite numbers by a central bank, no individual party has the ability to inflate the supply of bitcoin.
Decentralized Consensus
In the previous chapter we looked at the blockchain, the global list of all transactions, which everyone in the Bitcoin network accepts as the authoritative record of ownership transfers.
But how can everyone in the network agree on a single universal "truth" about who owns what, without having to trust anyone? All traditional payment systems depend on a trust model that has a central authority providing a clearinghouse service, basically verifying and clearing all transactions. Bitcoin has no central authority, yet somehow every full node has a complete copy of a public blockchain that it can trust as the authoritative record. The blockchain is not created by a central authority but is assembled independently by every node in the network. Somehow, every node in the network, acting on information transmitted across insecure network connections, can arrive at the same conclusion and assemble a copy of the same blockchain as everyone else. This chapter examines the process by which the Bitcoin network achieves global consensus without central authority.
One of Satoshi Nakamoto’s inventions is the decentralized mechanism for emergent consensus. Emergent because consensus is not achieved explicitly—there is no election or fixed moment when consensus occurs. Instead, consensus is an emergent artifact of the asynchronous interaction of thousands of independent nodes, all following simple rules. All the properties of Bitcoin, including currency, transactions, payments, and the security model that does not depend on central authority or trust, derive from this invention.
Bitcoin’s decentralized consensus emerges from the interplay of four processes that occur independently on nodes across the network:
-
Independent verification of each transaction, by every full node, based on a comprehensive list of criteria
-
Independent aggregation of those transactions into new blocks by mining nodes, coupled with demonstrated computation through a proof-of-work algorithm
-
Independent verification of the new blocks by every node and assembly into a chain
-
Independent selection, by every node, of the chain with the most cumulative computation demonstrated through proof of work
In the next few sections, we will examine these processes and how they interact to create the emergent property of network-wide consensus that allows any Bitcoin node to assemble its own copy of the authoritative, trusted, public, global blockchain.
Independent Verification of Transactions
In [c_transactions], we saw how wallet software creates transactions by collecting UTXOs, providing the appropriate authentication data, and then constructing new outputs assigned to a new owner. The resulting transaction is then sent to the neighboring nodes in the Bitcoin network so that it can be propagated across the entire Bitcoin network.
However, before forwarding transactions to its neighbors, every Bitcoin node that receives a transaction will first verify the transaction. This ensures that only valid transactions are propagated across the network, while invalid transactions are discarded at the first node that encounters them.
Each node verifies every transaction against a long checklist of criteria:
-
The transaction’s syntax and data structure must be correct.
-
Neither lists of inputs nor outputs are empty.
-
The transaction weight is low enough to allow it to fit in a block.
-
Each output value, as well as the total, must be within the allowed range of values (zero or more, but not exceeding 21 million bitcoins).
-
Lock time is equal to INT_MAX, or lock time and sequence values are satisfied according to the lock time and BIP68 rules.
-
The number of signature operations (SIGOPS) contained in the transaction is less than the signature operation limit.
-
The outputs being spent match outputs in the mempool or unspent outputs in a block in the main branch.
-
For each input, if the referenced output transaction is a coinbase output, it must have at least COINBASE_MATURITY (100) confirmations. Any absolute or relative lock time must also be satisfied. Nodes may relay transactions a block before they mature since they will be mature if included in the next block.
-
Reject if the sum of input values is less than sum of output values.
-
The scripts for each input must validate against the corresponding output scripts.
Note that the conditions change over time, to add new features or address new types of denial-of-service attacks.
By independently verifying each transaction as it is received and before propagating it, every node builds a pool of valid (but unconfirmed) transactions known as the memory pool or mempool.
Mining Nodes
Some of the nodes on the Bitcoin network are specialized nodes called miners. Jing is a Bitcoin miner; he earns bitcoin by running a "mining rig," which is a specialized computer-hardware system designed to mine bitcoin. Jing’s specialized mining hardware is connected to a server running a full node. Like every other full node, Jing’s node receives and propagates unconfirmed transactions on the Bitcoin network. Jing’s node, however, also aggregates these transactions into new blocks.
Let’s follow the blocks that were created during the time Alice made a purchase from Bob (see [spending_bitcoin]). For the purpose of demonstrating the concepts in this chapter, let’s assume the block containing Alice’s transaction was mined by Jing’s mining system and follow Alice’s transaction as it becomes part of this new block.
Jing’s mining node maintains a local copy of the blockchain. By the time Alice buys something, Jing’s node is caught up with the chain of blocks with the most proof of work. Jing’s node is listening for transactions, trying to mine a new block and also listening for blocks discovered by other nodes. As Jing’s node is mining, it receives a new block through the Bitcoin network. The arrival of this block signifies the end of the search for that block and the beginning of the search to create the next block.
During the previous several minutes, while Jing’s node was searching for a solution to the previous block, it was also collecting transactions in preparation for the next block. By now it has collected a few thousand transactions in its memory pool. Upon receiving the new block and validating it, Jing’s node will also compare it against all the transactions in the memory pool and remove any that were included in that block. Whatever transactions remain in the memory pool are unconfirmed and are waiting to be recorded in a new block.
Jing’s node immediately constructs a new partial block, a candidate for the next block. This block is called a candidate block because it is not yet a valid block, as it does not contain a valid proof-of-work. The block becomes valid only if the miner succeeds in finding a solution according to the proof-of-work algorithm.
When Jing’s node aggregates all the transactions from the memory pool, the new candidate block has several thousand transactions that each pay transaction fees he’ll attempt to claim.
The Coinbase Transaction
The first transaction in any block is a special transaction, called a coinbase transaction. This transaction is constructed by Jing’s node and pays out his reward for the mining effort.
Jing’s node creates the coinbase transaction as a payment to his own wallet. The total amount of reward that Jing collects for mining a block is the sum of the block subsidy (6.25 new bitcoins in 2023) and the transaction fees from all the transactions included in the block.
Unlike regular transactions, the coinbase transaction does not consume (spend) UTXOs as inputs. Instead, it has only one input, called the coinbase input, which implicitly contains the block reward. The coinbase transaction must have at least one output and may have as many outputs as will fit in the block. It’s common for coinbase transactions in 2023 to have two outputs: one of these is a zero-value output that uses OP_RETURN to commit to all of the witnesses for segregated witness (segwit) transactions in the block. The other output pays the miner their reward.
Coinbase Reward and Fees
To construct the coinbase transaction, Jing’s node first calculates the total amount of transaction fees:
Next, Jing’s node calculates the correct reward for the new block. The reward is calculated based on the block height, starting at 50 bitcoin per block and reduced by half every 210,000 blocks.
The calculation can be seen in function GetBlockSubsidy in the Bitcoin Core client, as shown in Calculating the block reward—Function GetBlockSubsidy, Bitcoin Core Client, main.cpp.
CAmount GetBlockSubsidy(int nHeight, const Consensus::Params& consensusParams)
{
int halvings = nHeight / consensusParams.nSubsidyHalvingInterval;
// Force block reward to zero when right shift is undefined.
if (halvings >= 64)
return 0;
CAmount nSubsidy = 50 * COIN;
// Subsidy is cut in half every 210,000 blocks.
nSubsidy >>= halvings;
return nSubsidy;
}The initial subsidy is calculated in satoshis by multiplying 50 with the COIN constant (100,000,000 satoshis). This sets the initial reward (nSubsidy) at 5 billion satoshis.
Next, the function calculates the number of halvings that have occurred by dividing the current block height by the halving interval (SubsidyHalvingInterval).
Next, the function uses the binary-right-shift operator to divide the reward (nSubsidy) by two for each round of halving. In the case of block 277,316, this would binary-right-shift the reward of 5 billion satoshis once (one halving) and result in 2.5 billion satoshis, or 25 bitcoins. After the 33rd halving, the subsidy will be rounded down to zero. The binary-right-shift operator is used because it is more efficient than multiple repeated divisions. To avoid a potential bug, the shift operation is skipped after 63 halvings, and the subsidy is set to 0.
Finally, the coinbase reward (nSubsidy) is added to the transaction fees (nFees), and the sum is returned.
|
Tip
|
If Jing’s mining node writes the coinbase transaction, what stops Jing from "rewarding" himself 100 or 1,000 bitcoin? The answer is that an inflated reward would result in the block being deemed invalid by everyone else, wasting Jing’s electricity used for PoW. Jing only gets to spend the reward if the block is accepted by everyone. |
Structure of the Coinbase Transaction
With these calculations, Jing’s node then constructs the coinbase transaction to pay himself the block reward.
The coinbase transaction has a special format. Instead of a transaction input specifying a previous UTXO to spend, it has a "coinbase" input. We examined transaction inputs in [inputs]. Let’s compare a regular transaction input with a coinbase transaction input. [table_8-1] shows the structure of a regular transaction, while [table_8-2] shows the structure of the coinbase transaction’s input.
| Size | Field | Description |
|---|---|---|
32 bytes |
Transaction Hash |
Pointer to the transaction containing the UTXO to be spent |
4 bytes |
Output Index |
The index number of the UTXO to be spent, first one is 0 |
1–9 bytes (compactSize) |
Script Size |
Script length in bytes, to follow |
Variable |
Input Script |
A script that fulfills the conditions of the UTXO output script |
4 bytes |
Sequence Number |
Multipurpose field used for BIP68 timelocks and transaction replacement signaling |
| Size | Field | Description |
|---|---|---|
32 bytes |
Transaction Hash |
All bits are zero: Not a transaction hash reference |
4 bytes |
Output Index |
All bits are ones: 0xFFFFFFFF |
1 byte |
Coinbase Data Size |
Length of the coinbase data, from 2 to 100 bytes |
Variable |
Coinbase Data |
Arbitrary data used for extra nonce and mining tags; in v2 blocks, must begin with block height |
4 bytes |
Sequence Number |
Set to 0xFFFFFFFF |
In a coinbase transaction, the first two fields are set to values that do not represent a UTXO reference. Instead of a "transaction hash," the first field is filled with 32 bytes all set to zero. The "output index" is filled with 4 bytes all set to 0xFF (255 decimal). The input script is replaced by coinbase data, a data field used by the miners, as we will see next.
Coinbase Data
Coinbase transactions do not have an input script field. Instead, this field is replaced by coinbase data, which must be between 2 and 100 bytes. Except for the first few bytes, the rest of the coinbase data can be used by miners in any way they want; it is arbitrary data.
In the genesis block, for example, Satoshi Nakamoto added the text "The Times 03/Jan/2009 Chancellor on brink of second bailout for banks" in the coinbase data, using it as a proof of the earliest date this block could have been created and to convey a message. Currently, miners often use the coinbase data to include extra nonce values and strings identifying the mining pool.
The first few bytes of the coinbase used to be arbitrary, but that is no longer the case. As per BIP34, version-2 blocks (blocks with the version field set to 2 or higher) must contain the block height as a script "push" operation in the beginning of the coinbase field.
Constructing the Block Header
To construct the block header, the mining node needs to fill in six fields, as listed in [block_header_structure_ch10].
| Size | Field | Description |
|---|---|---|
4 bytes |
Version |
A multipurpose bitfield |
32 bytes |
Previous Block Hash |
A reference to the hash of the previous (parent) block in the chain |
32 bytes |
Merkle Root |
A hash that is the root of the merkle tree of this block’s transactions |
4 bytes |
Timestamp |
The approximate creation time of this block (seconds from Unix Epoch) |
4 bytes |
Target |
The proof-of-work algorithm target for this block |
4 bytes |
Nonce |
A counter used for the proof-of-work algorithm |
The version field was originally an integer field and was used in three upgrades to the Bitcoin network, those defined in BIPs 34, 66, and 65. Each time, the version number was incremented. Later upgrades defined the version field as a bitfield, called versionbits, allowing up to 29 upgrades to be in progress simultaneously; see BIP9: Signaling and activation for details. Even later, miners began using some of the versionbits as an auxiliary nonce field.
|
Tip
|
The protocol upgrades defined in BIPs 34, 66, and 65 occurred in that order, with BIP66 (strict DER) occurring before BIP65 (OP_CHECKTIMELOCKVERIFY), so Bitcoin developers often list them in that order rather than sorted numerically. |
Today, the versionbits field has no meaning unless there’s an attempt to upgrade the consensus protocol underway, in which case you will need to read its documentation to determine how it is using versionbits.
Next, the mining node needs to add the "Previous Block Hash" (also known as prevhash). That is the hash of the block header of the previous block received from the network, which Jing’s node has accepted and selected as the parent of his candidate block.
|
Tip
|
By selecting the specific parent block, indicated by the Previous Block Hash field in the candidate block header, Jing is committing his mining power to extending the chain that ends in that specific block. |
The next step is to commit to all the transactions using merkle trees. Each transaction is listed using its witness transaction identifier (wtxid) in topographical order, with 32 0x00 bytes standing in for the wtxid of the first transaction (the coinbase). As we saw in the [merkle_trees] the last wtxid is hashed with itself if there are an odd number of wtxids, creating nodes that each contain the hash of one transaction. The transaction hashes are then combined, in pairs, creating each level of the tree, until all the transactions are summarized into one node at the "root" of the tree. The root of the merkle tree summarizes all the transactions into a single 32-byte value, which is the witness root hash.
The witness root hash is added to an output of the coinbase transaction. This step may be skipped if none of the transactions in the block are required to contain a witness structure. Each transaction (including the coinbase transaction) is then listed using its transaction identifier (txid) and used to build a second merkle tree, the root of which becomes the merkle root, to which the block header commits.
Jing’s mining node will then add a 4-byte timestamp, encoded as a Unix "epoch" timestamp, which is based on the number of seconds elapsed from January 1, 1970, midnight UTC/GMT.
Jing’s node then fills in the nBits target, which must be set to a compact representation of the required PoW to make this a valid block. The target is stored in the block as a "target bits" metric, which is a mantissa-exponent encoding of the target. The encoding has a 1-byte exponent, followed by a 3-byte mantissa (coefficient). In block 277,316, for example, the target bits value is 0x1903a30c. The first part 0x19 is a hexadecimal exponent, while the next part, 0x03a30c, is the coefficient. The concept of a target is explained in Retargeting to Adjust Difficulty and the "target bits" representation is explained in Target Representation.
The final field is the nonce, which is initialized to zero.
With all the other fields filled, the header of the candidate block is now complete and the process of mining can begin. The goal is now to find a header that results in a hash that is less than the target. The mining node will need to test billions or trillions of variations of the header before a version is found that satisfies the requirement.
Mining the Block
Now that a candidate block has been constructed by Jing’s node, it is time for Jing’s hardware mining rig to "mine" the block, to find a solution to the proof-of-work algorithm that makes the block valid. Throughout this book we have studied cryptographic hash functions as used in various aspects of the Bitcoin system. The hash function SHA256 is the function used in Bitcoin’s mining process.
In the simplest terms, mining is the process of hashing the candidate block header repeatedly, changing one parameter, until the resulting hash matches a specific target. The hash function’s result cannot be determined in advance, nor can a pattern be created that will produce a specific hash value. This feature of hash functions means that the only way to produce a hash result matching a specific target is to try again and again, modifying the input until the desired hash result appears by chance.
Proof-of-Work Algorithm
A hash algorithm takes an arbitrary-length data input and produces a fixed-length deterministic result, called a digest. The digest is a digital commitment to the input. For any specific input, the resulting digest will always be the same and can be easily calculated and verified by anyone implementing the same hash algorithm. A key characteristic of a cryptographic hash algorithm is that it is computationally infeasible to find two different inputs that produce the same digest (known as a collision). As a corollary, it is also virtually impossible to select an input in such a way as to produce a desired digest, other than trying random inputs.
With SHA256, the output is always 256 bits long, regardless of the size of the input. For example, we will calculate the SHA256 hash of the phrase, "Hello, World!":
$ echo "Hello, world!" | sha256sum d9014c4624844aa5bac314773d6b689ad467fa4e1d1a50a1b8a99d5a95f72ff5 -
This 256-bit output (represented in hex) is the hash or digest of the phrase and depends on every part of the phrase. Adding a single letter, punctuation mark, or any other character will produce a different hash.
A variable used in such a scenario is called a nonce. The nonce is used to vary the output of a cryptographic function, in this case to vary the output of the SHA256 commitment to the phrase.
To make a challenge out of this algorithm, let’s set a target: find a phrase that produces a hexadecimal hash that starts with a zero. Fortunately, this isn’t difficult, as shown in Simple proof-of-work implementation.
$ for nonce in $( seq 100 ) ; do echo "Hello, world! $nonce" | sha256sum ; done 3194835d60e85bf7f728f3e3f4e4e1f5c752398cbcc5c45e048e4dbcae6be782 - bfa474bbe2d9626f578d7d8c3acc1b604ec4a7052b188453565a3c77df41b79e - [...] f75a100821c34c84395403afd1a8135f685ca69ccf4168e61a90e50f47552f61 - 09cb91f8250df04a3db8bd98f47c7cecb712c99835f4123e8ea51460ccbec314 -
The phrase "Hello, World! 32" produces the following hash, which fits our criteria: 09cb91f8250df04a3db8bd98f47c7cecb712c99835f4123e8ea51460ccbec314. It took 32 attempts to find it. In terms of probabilities, if the output of the hash function is evenly distributed, we would expect to find a result with a 0 as the hexadecimal prefix once every 16 hashes (one out of 16 hexadecimal digits 0 through F). In numerical terms, that means finding a hash value that is less than 0x1000000000000000000000000000000000000000000000000000000000000000. We call this threshold the target, and the goal is to find a hash that is numerically less than the target. If we decrease the target, the task of finding a hash that is less than the target becomes more and more difficult.
To give a simple analogy, imagine a game where players throw a pair of dice repeatedly, trying to throw less than a specified target. In the first round, the target is 12. Unless you throw double-6, you win. In the next round the target is 11. Players must throw 10 or less to win, again an easy task. Let's say a few rounds later the target is down to 5. Now, more than half the dice throws will exceed the target and therefore be invalid. It takes more dice throws to win the lower the target gets. Eventually, when the target is 3 (the minimum possible), only one throw out of every 36, or about 3% of them, will produce a winning result.
From the perspective of an observer who knows that the target of the dice game is 3, if someone has succeeded in casting a winning throw it can be assumed that they attempted, on average, 36 throws. In other words, one can estimate the amount of work it takes to succeed from the difficulty imposed by the target. When the algorithm is based on a deterministic function such as SHA256, the input itself constitutes proof that a certain amount of work was done to produce a result below the target. Hence, proof of work.
|
Tip
|
Even though each attempt produces a random outcome, the probability of any possible outcome can be calculated in advance. Therefore, an outcome of specified difficulty constitutes proof of a specific amount of work. |
In Simple proof-of-work implementation, the winning "nonce" is 32, and this result can be confirmed by anyone independently. Anyone can add the number 32 as a suffix to the phrase "Hello, world!" and compute the hash, verifying that it is less than the target:
$ echo "Hello, world! 32" | sha256sum 09cb91f8250df04a3db8bd98f47c7cecb712c99835f4123e8ea51460ccbec314 -
Although it only takes one hash computation to verify, it took us 32 hash computations to find a nonce that worked. If we had a lower target (higher difficulty), it would take many more hash computations to find a suitable nonce, but only one hash computation for anyone to verify. And by knowing the target, anyone can estimate the difficulty using statistics and therefore know roughly how much work was needed to find such a nonce.
|
Tip
|
The PoW must produce a hash that is less than the target. A higher target means it is less difficult to find a hash that is below the target. A lower target means it is more difficult to find a hash below the target. The target and difficulty are inversely related. |
Bitcoin's PoW is very similar to the challenge shown in #sha256_example_generator_output2. The miner constructs a candidate block filled with transactions. Next, the miner calculates the hash of this block's header and sees if it is smaller than the current target. If the hash is not less than the target, the miner will modify the nonce (usually just incrementing it by one) and try again. At the current difficulty in the Bitcoin network, miners have to try a huge number of times before finding a nonce that results in a low enough block header hash.
Target Representation
Block headers contain the target in a notation called "target bits" or just "bits," which in block 277,316 has the value of 0x1903a30c. This notation expresses the proof-of-work target as a coefficient/exponent format, with the first two hexadecimal digits for the exponent and the next six hex digits as the coefficient. In this block, therefore, the exponent is 0x19 and the coefficient is 0x03a30c.
The formula to calculate the difficulty target from this representation is:
- target = coefficient × 2(8 × (exponent – 3))
Using that formula, and the difficulty bits value 0x1903a30c, we get:
- target = 0x03a30c × 20x08 × (0x19 – 0x03)
which is:
- 22,829,202,948,393,929,850,749,706,076,701,368,331,072,452,018,388,575,715,328
Or, in hexadecimal:
- 0x0000000000000003A30C00000000000000000000000000000000000000000000
This means that a valid block for height 277,316 is one that has a block header hash less than the target. In binary that number must have more than 60 leading bits set to zero. With this level of difficulty, a single miner processing 1 trillion hashes per second (1 terahash per second or 1 TH/sec) would only find a solution once every 8,496 blocks or once every 59 days, on average.
Retargeting to Adjust Difficulty
As we saw, the target determines the difficulty and therefore affects how long it takes to find a solution to the proof-of-work algorithm. This leads to the obvious questions: Why is the difficulty adjustable, who adjusts it, and how?
Bitcoin’s blocks are generated every 10 minutes, on average. This is Bitcoin’s heartbeat and underpins the frequency of currency issuance and the speed of transaction settlement. It has to remain constant not just over the short term, but over a period of many decades. Over this time, it is expected that computer power will continue to increase at a rapid pace. Furthermore, the number of participants in mining and the computers they use will also constantly change. To keep the block generation time at 10 minutes, the difficulty of mining must be adjusted to account for these changes. In fact, the proof-of-work target is a dynamic parameter that is periodically adjusted to meet a 10-minute block interval goal. In simple terms, the target is set so that the current mining power will result in a 10-minute block interval.
How, then, is such an adjustment made in a completely decentralized network? Retargeting occurs automatically and on every node independently. Every 2,016 blocks, all nodes retarget the PoW. The ratio between the actual time span and desired time span of 10 minutes per block is calculated and a proportionate adjustment (up or down) is made to the target. In simple terms: If the network is finding blocks faster than every 10 minutes, the difficulty increases (target decreases). If block discovery is slower than expected, the difficulty decreases (target increases).
The equation can be summarized as:
New Target = Old Target * (20,160 minutes / Actual Time of Last 2015 Blocks)
|
Note
|
While the target calibration happens every 2,016 blocks, because of an off-by-one error in the original Bitcoin software, it is based on the total time of the previous 2,015 blocks (not 2,016 as it should be), resulting in a retargeting bias toward higher difficulty by 0.05%. |
Retargeting the proof of work: CalculateNextWorkRequired() in pow.cpp shows the code used in the Bitcoin Core client.
// Limit adjustment step
int64_t nActualTimespan = pindexLast->GetBlockTime() - nFirstBlockTime;
LogPrintf(" nActualTimespan = %d before bounds\n", nActualTimespan);
if (nActualTimespan < params.nPowTargetTimespan/4)
nActualTimespan = params.nPowTargetTimespan/4;
if (nActualTimespan > params.nPowTargetTimespan*4)
nActualTimespan = params.nPowTargetTimespan*4;
// Retarget
const arith_uint256 bnPowLimit = UintToArith256(params.powLimit);
arith_uint256 bnNew;
arith_uint256 bnOld;
bnNew.SetCompact(pindexLast->nBits);
bnOld = bnNew;
bnNew *= nActualTimespan;
bnNew /= params.nPowTargetTimespan;
if (bnNew > bnPowLimit)
bnNew = bnPowLimit;The parameters Interval (2,016 blocks) and TargetTimespan (two weeks as 1,209,600 seconds) are defined in chainparams.cpp.
To avoid extreme volatility in the difficulty, the retargeting adjustment must be less than a factor of four (4) per cycle. If the required target adjustment is greater than a factor of four, it will be adjusted by a factor of 4 and not more. Any further adjustment will be accomplished in the next retargeting period because the imbalance will persist through the next 2,016 blocks. Therefore, large discrepancies between hashing power and difficulty might take several 2,016-block cycles to balance out.
Note that the target is independent of the number of transactions or the value of transactions. This means that the amount of hashing power and therefore electricity expended to secure bitcoin is also entirely independent of the number of transactions. Bitcoin can scale up and remain secure without any increase in hashing power from today’s level. The increase in hashing power represents market forces as new miners enter the market. As long as enough hashing power is under the control of miners acting honestly in pursuit of the reward, it is enough to prevent "takeover" attacks and, therefore, it is enough to secure bitcoin.
The difficulty of mining is closely related to the cost of electricity and the exchange rate of bitcoin vis-a-vis the currency used to pay for electricity. High-performance mining systems are about as efficient as possible with the current generation of silicon fabrication, converting electricity into hashing computation at the highest rate possible. The primary influence on the mining market is the price of one kilowatt-hour of electricity in bitcoin because that determines the profitability of mining and therefore the incentives to enter or exit the mining market.
Median Time Past (MTP)
In Bitcoin there is a subtle, but very significant, difference between wall time and consensus time. Bitcoin is a decentralized network, which means that each participant has his or her own perspective of time. Events on the network do not occur instantaneously everywhere. Network latency must be factored into the perspective of each node. Eventually everything is synchronized to create a common blockchain. Bitcoin reaches consensus every 10 minutes about the state of the blockchain as it existed in the past.
The timestamps set in block headers are set by the miners. There is a certain degree of latitude allowed by the consensus rules to account for differences in clock accuracy between decentralized nodes. However, this creates an unfortunate incentive for miners to lie about the time in a block. For example, if a miner sets their time in the future, they can lower difficulty, allowing them to mine more blocks and claim some of the block subsidy reserved for future miners. If they can set their times in the past for some blocks, they can use the current time for some other blocks, and so again make it look like there's a long time between blocks for the purpose of manipulating difficulty.
To prevent manipulation, Bitcoin has two consensus rules. The first is that no node will accept any block with a time further in the future than two hours. The second is that no node will accept a block with a time less than or equal to the median time of the last 11 blocks, called median time past (MTP).
As part of the activation of BIP68 relative timelocks, there was also a change in the way "time" is calculated for timelocks (both absolute and relative) in transactions. Previously, a miner could include any transaction in a block with a timelock equal to or below the time of the block. That incentivized miners to use the latest time they thought was possible (close to two hours in the future) so that more transactions would be eligible for their block.
To remove the incentive to lie and strengthen the security of timelocks, BIP113 was proposed and activated at the same time as the BIPs for relative timelocks. The MTP became the consensus time used for all timelock calculations. By taking the midpoint from approximately two hours in the past, the influence of any one block’s timestamp is reduced. By incorporating 11 blocks, no single miner can influence the timestamps in order to gain fees from transactions with a timelock that hasn’t yet matured.
MTP changes the implementation of time calculations for lock time, CLTV, sequence, and CSV. The consensus time calculated by MTP is usually about one hour behind wall clock time. If you create timelock transactions, you should account for it when estimating the desired value to encode in lock time, sequence, CLTV, and CSV.
Successfully Mining the Block
As we saw earlier, Jing's node has constructed a candidate block and prepared it for mining. Jing has several hardware mining rigs with application-specific integrated circuits, where hundreds of thousands of integrated circuits run Bitcoin's double SHA256 algorithm in parallel at incredible speeds. Many of these specialized machines are connected to his mining node over USB or a local area network. Next, the mining node running on Jing's desktop transmits the block header to his mining hardware, which starts testing trillions of variations of the header per second. Because the nonce is only 32 bits, after exhausting all the nonce possibilities (about 4 billion), the mining hardware changes the block header (adjusting the coinbase extra nonce space, versionbits, or timestamp) and resets the nonce counter, testing new combinations.
Almost 11 minutes after starting to mine a particular block, one of the hardware mining machines finds a solution and sends it back to the mining node.
Immediately, Jing’s mining node transmits the block to all its peers. They receive, validate, and then propagate the new block. As the block ripples out across the network, each node adds it to its own copy of the blockchain, extending it to a new height. As mining nodes receive and validate the block, they abandon their efforts to find a block at the same height and immediately start computing the next block in the chain, using Jing’s block as the "parent." By building on top of Jing’s newly discovered block, the other miners are essentially using their mining power to endorse Jing’s block and the chain it extends.
In the next section, we’ll look at the process each node uses to validate a block and select the most-work chain, creating the consensus that forms the decentralized blockchain.
Validating a New Block
The third step in Bitcoin’s consensus mechanism is independent validation of each new block by every node on the network. As the newly solved block moves across the network, each node performs a series of tests to validate it. The independent validation also ensures that only blocks that follow the consensus rules are incorporated in the blockchain, thus earning their miners the reward. Blocks that violate the rules are rejected and not only lose their miners the reward, but also waste the effort expended to find a proof-of-work solution, thus incurring upon those miners all of the costs of creating a block but giving them none of the rewards.
When a node receives a new block, it will validate the block by checking it against a long list of criteria that must all be met; otherwise, the block is rejected. These criteria can be seen in the Bitcoin Core client in the functions CheckBlock and CheckBlockHeader and include:
-
The block data structure is syntactically valid.
-
The block header hash is less than the target (enforces the proof of work).
-
The block timestamp is between the MTP and two hours in the future (allowing for time errors).
-
The block weight is within acceptable limits.
-
The first transaction (and only the first) is a coinbase transaction.
-
All transactions within the block are valid using the transaction checklist discussed in Independent Verification of Transactions.
The independent validation of each new block by every node on the network ensures that the miners cannot cheat. In previous sections we saw how miners get to write a transaction that awards them the new bitcoin created within the block and claim the transaction fees. Why don’t miners write themselves a transaction for a thousand bitcoins instead of the correct reward? Because every node validates blocks according to the same rules. An invalid coinbase transaction would make the entire block invalid, which would result in the block being rejected and, therefore, that transaction would never become part of the blockchain. The miners have to construct a block, based on the shared rules that all nodes follow, and mine it with a correct solution to the PoW. To do so, they expend a lot of electricity in mining, and if they cheat, all the electricity and effort is wasted. This is why independent validation is a key component of decentralized consensus.
Assembling and Selecting Chains of Blocks
The final part in Bitcoin’s decentralized consensus mechanism is the assembly of blocks into chains and the selection of the chain with the most proof of work.
A best blockchain is whichever valid chain of blocks has the most cumulative PoW associated with it. The best chain may also have branches with blocks that are "siblings" to the blocks on the best chain. These blocks are valid but not part of the best chain. They are kept for future reference in case one of those secondary chains later becomes primary. When sibling blocks occur, they’re usually the result of an almost simultaneous mining of different blocks at the same height.
When a new block is received, a node will try to add it onto the existing blockchain. The node will look at the block’s "previous block hash" field, which is the reference to the block’s parent. Then, the node will attempt to find that parent in the existing blockchain. Most of the time, the parent will be the "tip" of the best chain, meaning this new block extends the best chain.
Sometimes the new block does not extend the best chain. In that case, the node will attach the new block’s header to a secondary chain and then compare the work of the secondary chain to the previous best chain. If the secondary chain is now the best chain, the node will accordingly reorganize its view of confirmed transactions and available UTXOs. If the node is a miner, it will now construct a candidate block extending this new, more-proof-of-work, chain.
By selecting the greatest-cumulative-work valid chain, all nodes eventually achieve network-wide consensus. Temporary discrepancies between chains are resolved eventually as more work is added, extending one of the possible chains.
|
Tip
|
The blockchain forks described in this section occur naturally as a result of transmission delays in the global network. We will also look at deliberately induced forks later in this chapter. |
Forks are almost always resolved within one block. It is possible for an accidental fork to extend to two blocks if both blocks are found almost simultaneously by miners on opposite "sides" of a previous fork. However, the chance of that happening is low.
Bitcoin’s block interval of 10 minutes is a design compromise between fast confirmation times and the probability of a fork. A faster block time would make transactions seem to clear faster but lead to more frequent blockchain forks, whereas a slower block time would decrease the number of forks but make settlement seem slower.
|
Note
|
Which is more secure: a transaction included in one block where the average time between blocks is 10 minutes, or a transaction included in a block with nine blocks built on top of it where the average time between blocks is one minute? The answer is that they’re equally secure. A malicious miner wanting to double spend that transaction would need to do an amount of work equal to 10 minutes of the total network hash rate in order to create a chain with equal proof of work. Shorter times between blocks doesn’t result in earlier settlement. Its only advantage is providing weaker guarantees to people who are willing to accept those guarantees. For example, if you’re willing to accept three minutes of miners agreeing on the best blockchain as sufficient security, you’d prefer a system with 1-minute blocks, where you could wait for three blocks, over a system with 10-minute blocks. The shorter the time between blocks, the more miner work is wasted on accidental forks (in addition to other problems), so many people prefer Bitcoin’s 10-minute blocks over shorter block intervals. |
Mining and the Hash Lottery
Bitcoin mining is an extremely competitive industry. The hashing power has increased exponentially every year of Bitcoin’s existence. Some years the growth has reflected a complete change of technology, such as in 2010 and 2011 when many miners switched from using CPU mining to GPU mining and field programmable gate array (FPGA) mining. In 2013 the introduction of ASIC mining led to another giant leap in mining power, by placing the double-SHA256 function directly on silicon chips specialized for the purpose of mining. The first such chips could deliver more mining power in a single box than the entire Bitcoin network in 2010.
At the time of writing, it is believed that there are no more giant leaps left in Bitcoin mining equipment because the industry has reached the forefront of Moore’s Law, which stipulates that computing density will double approximately every 18 months. Still, the mining power of the network continues to advance at a rapid pace.
The Extra Nonce Solution
Since 2012, mining has evolved to resolve a fundamental limitation in the structure of the block header. In the early days of Bitcoin, a miner could find a block by iterating through the nonce until the resulting hash was below the target. As difficulty increased, miners often cycled through all 4 billion values of the nonce without finding a block. However, this was easily resolved by updating the block timestamp to account for the elapsed time. Because the timestamp is part of the header, the change would allow miners to iterate through the values of the nonce again with different results. Once mining hardware exceeded 4 GH/sec, however, this approach became increasingly difficult because the nonce values were exhausted in less than a second. As ASIC mining equipment started exceeding the TH/sec hash rate, the mining software needed more space for nonce values in order to find valid blocks. The timestamp could be stretched a bit, but moving it too far into the future would cause the block to become invalid. A new source of variation was needed in the block header.
One solution that was widely implemented was to use the coinbase transaction as a source of extra nonce values. Because the coinbase script can store between 2 and 100 bytes of data, miners started using that space as extra nonce space, allowing them to explore a much larger range of block header values to find valid blocks. The coinbase transaction is included in the merkle tree, which means that any change in the coinbase script causes the merkle root to change. Eight bytes of extra nonce, plus the 4 bytes of "standard" nonce, allow miners to explore a total 296 (8 followed by 28 zeros) possibilities per second without having to modify the timestamp.
Another solution widely used today is to use up to 16 bits of the block header versionbits field for mining, as described in BIP320. If each piece of mining equipment has its own coinbase transaction, this allows an individual piece of mining equipment to perform up to 281 TH/s by only making changes to the block header. This keeps mining equipment and protocols simpler than incrementing the extra nonce in the coinbase transaction every 4 billion hashes, which requires recalculating the entire left flank of the merkle tree up to the root.
Mining Pools
In this highly competitive environment, individual miners working alone (also known as solo miners) don’t stand a chance. The likelihood of them finding a block to offset their electricity and hardware costs is so low that it represents a gamble, like playing the lottery. Even the fastest consumer ASIC mining system cannot keep up with commercial operations that stack tens of thousands of these systems in giant warehouses near powerstations. Many miners now collaborate to form mining pools, pooling their hashing power and sharing the reward among thousands of participants. By participating in a pool, miners get a smaller share of the overall reward, but typically get rewarded every day, reducing uncertainty.
Let’s look at a specific example. Assume a miner has purchased mining hardware with a combined hashing rate of 0.0001% of current the total network hash rate. If the protocol difficulty never changes, that miner will find a new block approximately once every 20 years. That’s a potentially long time to wait to get paid. However, if that miner works together in a mining pool with other miners whose aggregate hash rate is 1% of the total network hash rate, they’ll average more than one block per day. That miner will only receive their portion of the rewards (minus any fees charged by the pool), so they’ll only receive a small amount per day. If they mined every day for 20 years, they’d earn the same amount (not counting pool fees) as if they found an average block on their own. The only fundamental difference is the frequency of the payments they receive.
Mining pools coordinate many hundreds or thousands of miners over specialized pool-mining protocols. The individual miners configure their mining equipment to connect to a pool server, after creating an account with the pool. Their mining hardware remains connected to the pool server while mining, synchronizing their efforts with the other miners. Thus, the pool miners share the effort to mine a block and then share in the rewards.
Successful blocks pay the reward to a pool Bitcoin address rather than to individual miners. The pool server will periodically make payments to the miners' Bitcoin addresses once their share of the rewards has reached a certain threshold. Typically, the pool server charges a percentage fee of the rewards for providing the pool-mining service.
Miners participating in a pool split the work of searching for a solution to a candidate block, earning "shares" for their mining contribution. The mining pool sets a higher target (lower difficulty) for earning a share, typically more than 1,000 times easier than the Bitcoin network’s target. When someone in the pool successfully mines a block, the reward is earned by the pool and then shared with all miners in proportion to the number of shares they contributed to the effort.
Many pools are open to any miner, big or small, professional or amateur. A pool will therefore have some participants with a single small mining machine, and others with a garage full of high-end mining hardware. Some will be mining with a few tens of a kilowatt of electricity, others will be running a data center consuming megawatts of power. How does a mining pool measure the individual contributions, so as to fairly distribute the rewards, without the possibility of cheating? The answer is to use Bitcoin’s proof-of-work algorithm to measure each pool miner’s contribution, but set at a lower difficulty so that even the smallest pool miners win a share frequently enough to make it worthwhile to contribute to the pool. By setting a lower difficulty for earning shares, the pool measures the amount of work done by each miner. Each time a pool miner finds a block header hash that is less than the pool target, they prove they have done the hashing work to find that result. That header ultimately commits to the coinbase transaction and can be used to prove the miner used a coinbase transaction that would have paid the block reward to the pool. Each pool miner is given a slightly different coinbase transaction template so each of them hashes different candidate block headers, preventing duplication of effort.
The work to find shares contributes, in a statistically measurable way, to the overall effort to find a hash lower than the Bitcoin network’s target. Thousands of miners trying to find low-value hashes will eventually find one low enough to satisfy the Bitcoin network target.
Let’s return to the analogy of a dice game. If the dice players are throwing dice with a goal of throwing less than four (the overall network difficulty), a pool would set an easier target, counting how many times the pool players managed to throw less than eight. When pool players throw less than eight (the pool share target), they earn shares, but they don’t win the game because they don’t achieve the game target (less than four). The pool players will achieve the easier pool target much more often, earning them shares very regularly, even when they don’t achieve the harder target of winning the game. Every now and then, one of the pool players will throw a combined dice throw of less than four and the pool wins. Then, the earnings can be distributed to the pool players based on the shares they earned. Even though the target of eight-or-less wasn’t winning, it was a fair way to measure dice throws for the players, and it occasionally produces a less-than-four throw.
Similarly, a mining pool will set a (higher and easier) pool target that will ensure that an individual pool miner frequently earns shares by finding block header hashes that are less than the pool target. Every now and then, one of these attempts will produce a block header hash that is less than the Bitcoin network target, making it a valid block and the whole pool wins.
Managed pools
Most mining pools are "managed," meaning that there is a company or individual running a pool server. The owner of the pool server is called the pool operator, and they charge pool miners a percentage fee of the earnings.
The pool server runs specialized software and a pool-mining protocol that coordinate the activities of the pool miners. The pool server is also connected to one or more full Bitcoin nodes. This allows the pool server to validate blocks and transactions on behalf of the pool miners, relieving them of the burden of running a full node. For some miners, the ability to mine without running a full node is another benefit of joining a managed pool.
Pool miners connect to the pool server using a mining protocol such as Stratum (either version 1 or version 2). Stratum v1 creates block templates that contain a template of a candidate block header. The pool server constructs a candidate block by aggregating transactions, adding a coinbase transaction (with extra nonce space), calculating the merkle root, and linking to the previous block hash. The header of the candidate block is then sent to each of the pool miners as a template. Each pool miner then mines using the block template, at a higher (easier) target than the Bitcoin network target, and sends any successful results back to the pool server to earn shares.
Stratum v2 optionally allows individual miners in the pool to choose which transactions appear in their own blocks, which they can select using their own full node.
Peer-to-peer mining pool (P2Pool)
Managed pools using Stratum v1 create the possibility of cheating by the pool operator, who might direct the pool effort to double-spend transactions or invalidate blocks (see Hashrate Attacks). Furthermore, centralized pool servers represent a single point of failure. If the pool server is down or is slowed by a denial-of-service attack, the pool miners cannot mine. In 2011, to resolve these issues of centralization, a new pool mining method was proposed and implemented: P2Pool, a peer-to-peer mining pool without a central operator.
P2Pool works by decentralizing the functions of the pool server, implementing a parallel blockchain-like system called a share chain. A share chain is a blockchain running at a lower difficulty than the Bitcoin blockchain. The share chain allows pool miners to collaborate in a decentralized pool by mining shares on the share chain at a rate of one share block every 30 seconds. Each of the blocks on the share chain records a proportionate share reward for the pool miners who contribute work, carrying the shares forward from the previous share block. When one of the share blocks also achieves the Bitcoin network target, it is propagated and included on the Bitcoin blockchain, rewarding all the pool miners who contributed to all the shares that preceded the winning share block. Essentially, instead of a pool server keeping track of pool miner shares and rewards, the share chain allows all pool miners to keep track of all shares using a decentralized consensus mechanism like Bitcoin’s blockchain consensus mechanism.
P2Pool mining is more complex than pool mining because it requires that the pool miners run a dedicated computer with enough disk space, memory, and internet bandwidth to support a Bitcoin full node and the P2Pool node software. P2Pool miners connect their mining hardware to their local P2Pool node, which simulates the functions of a pool server by sending block templates to the mining hardware. On P2Pool, individual pool miners construct their own candidate blocks, aggregating transactions much like solo miners, but then mine collaboratively on the share chain. P2Pool is a hybrid approach that has the advantage of much more granular payouts than solo mining, but without giving too much control to a pool operator like managed pools.
Even though P2Pool reduces the concentration of power by mining pool operators, it is conceivably vulnerable to 51% attacks against the share chain itself. A much broader adoption of P2Pool does not solve the 51% attack problem for Bitcoin itself. Rather, P2Pool makes Bitcoin more robust overall, as part of a diversified mining ecosystem. As of this writing, P2Pool has fallen into disuse, but new protocols such as Stratum v2 can allow individual miners to choose the transactions they include in their blocks.
Hashrate Attacks
Bitcoin’s consensus mechanism is, at least theoretically, vulnerable to attack by miners (or pools) that attempt to use their hashing power to dishonest or destructive ends. As we saw, the consensus mechanism depends on having a majority of the miners acting honestly out of self-interest. However, if a miner or group of miners can achieve a significant share of the mining power, they can attack the consensus mechanism so as to disrupt the security and availability of the Bitcoin network.
It is important to note that hashrate attacks have the greatest effect on future consensus. Confirmed transactions on the best blockchain become more and more immutable as time passes. While in theory, a fork can be achieved at any depth, in practice, the computing power needed to force a very deep fork is immense, making old blocks very hard to change. Hashrate attacks also do not affect the security of the private keys and signing algorithms.
One attack scenario against the consensus mechanism is called the majority attack or 51% attack. In this scenario a group of miners, controlling a majority of the total network’s hashing power (such as 51%), collude to attack Bitcoin. With the ability to mine the majority of the blocks, the attacking miners can cause deliberate "forks" in the blockchain and double-spend transactions or execute denial-of-service attacks against specific transactions or addresses. A fork/double-spend attack is where the attacker causes previously confirmed blocks to be invalidated by forking below them and reconverging on an alternate chain. With sufficient power, an attacker can invalidate six or more blocks in a row, causing transactions that were considered immutable (six confirmations) to be invalidated. Note that a double-spend can only be done on the attacker’s own transactions, for which the attacker can produce a valid signature. Double-spending one’s own transactions can be profitable if invalidating a transaction allows the attacker to get an irreversible exchange payment or product without paying for it.
Let’s examine a practical example of a 51% attack. In the first chapter, we looked at a transaction between Alice and Bob. Bob, the seller, is willing to accept payment without waiting for confirmation (mining in a block) because the risk of a double-spend on a small item is low in comparison to the convenience of rapid customer service. This is similar to the practice of coffee shops that accept credit card payments without a signature for amounts below $25, because the risk of a credit-card chargeback is low while the cost of delaying the transaction to obtain a signature is comparatively larger. In contrast, selling a more expensive item for bitcoins runs the risk of a double-spend attack, where the buyer broadcasts a competing transaction that spends one of the same inputs (UTXOs) and cancels the payment to the merchant. A 51% attack allows attackers to double-spend their own transactions in the new chain, thus undoing the corresponding transaction in the old chain.
In our example, malicious attacker Mallory goes to Carol’s gallery and purchases a set of beautiful paintings depicting Satoshi Nakamoto as Prometheus. Carol sells the paintings for $250,000 in bitcoins to Mallory. Instead of waiting for six or more confirmations on the transaction, Carol wraps and hands the paintings to Mallory after only one confirmation. Mallory works with an accomplice, Paul, who operates a large mining pool, and the accomplice launches an attack as soon as Mallory’s transaction is included in a block. Paul directs the mining pool to remine the same block height as the block containing Mallory’s transaction, replacing Mallory’s payment to Carol with a transaction that double-spends the same input as Mallory’s payment. The double-spend transaction consumes the same UTXO and pays it back to Mallory’s wallet instead of paying it to Carol, essentially allowing Mallory to keep the bitcoins. Paul then directs the mining pool to mine an additional block, so as to make the chain containing the double-spend transaction longer than the original chain (causing a fork below the block containing Mallory’s transaction). When the blockchain fork resolves in favor of the new (longer) chain, the double-spent transaction replaces the original payment to Carol. Carol is now missing the three paintings and also has no payment. Throughout all this activity, Paul’s mining pool participants might remain blissfully unaware of the double-spend attempt because they mine with automated miners and cannot monitor every transaction or block.
To protect against this kind of attack, a merchant selling large-value items must wait at least six confirmations before giving the product to the buyer. Waiting for more than six confirmations may sometimes be warranted. Alternatively, the merchant should use an escrow multisignature account, again waiting for several confirmations after the escrow account is funded. The more confirmations elapse, the harder it becomes to invalidate a transaction by reorganizing the blockchain. For high-value items, payment by bitcoin will still be convenient and efficient even if the buyer has to wait 24 hours for delivery, which would correspond to approximately 144 confirmations.
In addition to a double-spend attack, the other scenario for a consensus attack is to deny service to specific participants (specific Bitcoin addresses). An attacker with a majority of the mining power can censor transactions. If they are included in a block mined by another miner, the attacker can deliberately fork and remine that block, again excluding the specific transactions. This type of attack can result in a sustained denial-of-service against a specific address or set of addresses for as long as the attacker controls the majority of the mining power.
Despite its name, the 51% attack scenario doesn’t actually require 51% of the hashing power. In fact, such an attack can be attempted with a smaller percentage of the hashing power. The 51% threshold is simply the level at which such an attack is almost guaranteed to succeed. A hashrate attack is essentially a tug-of-war for the next block, and the "stronger" group is more likely to win. With less hashing power, the probability of success is reduced because other miners control the generation of some blocks with their "honest" mining power. One way to look at it is that the more hashing power an attacker has, the longer the fork he can deliberately create, the more blocks in the recent past he can invalidate, or the more blocks in the future he can control. Security research groups have used statistical modeling to claim that various types of hashrate attacks are possible with as little as 30% of the hashing power.
The centralization of control caused by mining pools has introduced the risk of for-profit attacks by a mining pool operator. The pool operator in a managed pool controls the construction of candidate blocks and also controls which transactions are included. This gives the pool operator the power to exclude transactions or introduce double-spend transactions. If such abuse of power is done in a limited and subtle way, a pool operator could conceivably profit from a hashrate attack without being noticed.
Not all attackers will be motivated by profit, however. One potential attack scenario is where an attacker intends to disrupt the Bitcoin network without the possibility of profiting from such disruption. A malicious attack aimed at crippling Bitcoin would require enormous investment and covert planning but could conceivably be launched by a well-funded, most likely state-sponsored, attacker. Alternatively, a well-funded attacker could attack Bitcoin by simultaneously amassing mining hardware, compromising pool operators, and attacking other pools with denial-of-service. All of these scenarios are theoretically possible.
Undoubtedly, a serious hashrate attack would erode confidence in Bitcoin in the short term, possibly causing a significant price decline. However, the Bitcoin network and software are constantly evolving, so attacks would be met with countermeasures by the Bitcoin community.
Changing the Consensus Rules
The rules of consensus determine the validity of transactions and blocks. These rules are the basis for collaboration between all Bitcoin nodes and are responsible for the convergence of all local perspectives into a single consistent blockchain across the entire network.
While the consensus rules are invariable in the short term and must be consistent across all nodes, they are not invariable in the long term. In order to evolve and develop the Bitcoin system, the rules can change from time to time to accommodate new features, improvements, or bug fixes. Unlike traditional software development, however, upgrades to a consensus system are much more difficult and require coordination between all participants.
Hard Forks
In Assembling and Selecting Chains of Blocks we looked at how the Bitcoin network may briefly diverge, with two parts of the network following two different branches of the blockchain for a short time. We saw how this process occurs naturally, as part of the normal operation of the network and how the network converges on a common blockchain after one or more blocks are mined.
There is another scenario in which the network may diverge into following two chains: a change in the consensus rules. This type of fork is called a hard fork, because after the fork, the network may not converge onto a single chain. Instead, the two chains can evolve independently. Hard forks occur when part of the network is operating under a different set of consensus rules than the rest of the network. This may occur because of a bug or because of a deliberate change in the implementation of the consensus rules.
Hard forks can be used to change the rules of consensus, but they require coordination between all participants in the system. Any nodes that do not upgrade to the new consensus rules are unable to participate in the consensus mechanism and are forced onto a separate chain at the moment of the hard fork. Thus, a change introduced by a hard fork can be thought of as not "forward compatible," in that nonupgraded systems can no longer process blocks because of the new consensus rules.
Let’s examine the mechanics of a hard fork with a specific example.
A blockchain with forks. shows a blockchain with two forks. At block height 4, a one-block fork occurs. This is the type of spontaneous fork we saw in Assembling and Selecting Chains of Blocks. With the mining of block 5, the network converges on one chain and the fork is resolved.
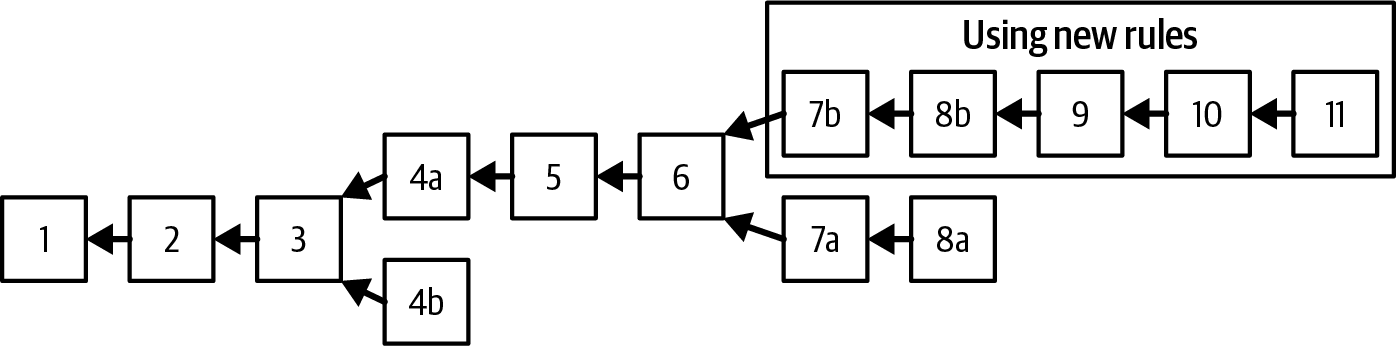
Later, however, at block height 6, a new implementation of the client is released with a change in the consensus rules. Starting on block height 7, miners running this new implementation will accept a new type of bitcoin; let’s call it a "foocoin." Immediately after, a node running the new implementation creates a transaction that contains a foocoin and a miner with the updated software mines block 7b containing this transaction.
Any node or miner that has not upgraded the software to validate foocoin is now unable to process block 7b. From their perspective, both the transaction that contained a foocoin and block 7b that contained that transaction are invalid because they are evaluating them based upon the old consensus rules. These nodes will reject the transaction and the block and will not propagate them. Any miners that are using the old rules will not accept block 7b and will continue to mine a candidate block whose parent is block 6. In fact, miners using the old rules may not even receive block 7b if all the nodes they are connected to are also obeying the old rules and therefore not propagating the block. Eventually, they will be able to mine block 7a, which is valid under the old rules and does not contain any transactions with foocoins.
The two chains continue to diverge from this point. Miners on the "b" chain will continue to accept and mine transactions containing foocoins, while miners on the "a" chain will continue to ignore these transactions. Even if block 8b does not contain any foocoin transactions, the miners on the "a" chain cannot process it. To them it appears to be an invalid block, as its parent "7b" is not recognized as a valid block.
Hard forks: Software, network, mining, and chain
For software developers, the term "fork" has another meaning, adding confusion to the term "hard fork." In open source software, a fork occurs when a group of developers choose to follow a different software roadmap and start a competing implementation of an open source project. We’ve already discussed two circumstances that will lead to a hard fork: a bug in the consensus rules and a deliberate modification of the consensus rules. In the case of a deliberate change to the consensus rules, a software fork precedes the hard fork. However, for this type of hard fork to occur, a new software implementation of the consensus rules must be developed, adopted, and launched.
Examples of software forks that have attempted to change consensus rules include Bitcoin XT and Bitcoin Classic. However, neither of those programs resulted in a hard fork. While a software fork is a necessary precondition, it is not in itself sufficient for a hard fork to occur. For a hard fork to occur, the competing implementation must be adopted and the new rules activated, by miners, wallets, and intermediary nodes. Conversely, there are numerous alternative implementations of Bitcoin Core, and even software forks, that do not change the consensus rules and barring a bug, can coexist on the network and interoperate without causing a hard fork.
Consensus rules may differ in obvious and explicit ways, in the validation of transactions or blocks. The rules may also differ in more subtle ways, in the implementation of the consensus rules as they apply to Bitcoin scripts or cryptographic primitives such as digital signatures. Finally, the consensus rules may differ in unanticipated ways because of implicit consensus constraints imposed by system limitations or implementation details. An example of the latter was seen in the unanticipated hard fork during the upgrade of Bitcoin Core 0.7 to 0.8, which was caused by a limitation in the Berkeley DB implementation used to store blocks.
Conceptually, we can think of a hard fork as developing in four stages: a software fork, a network fork, a mining fork, and a chain fork. The process begins when an alternative implementation of the client, with modified consensus rules, is created by developers.
When this forked implementation is deployed in the network, a certain percentage of miners, wallet users, and intermediate nodes may adopt and run this implementation. First, the network will fork. Nodes based on the original implementation of the consensus rules will reject any transactions and blocks that are created under the new rules. Furthermore, the nodes following the original consensus rules may disconnect from any nodes that are sending them these invalid transactions and blocks. As a result, the network may partition into two: old nodes will only remain connected to old nodes and new nodes will only be connected to new nodes. A single block based on the new rules will ripple through the network and result in a partition into two networks.
New miners may mine on top of the new block, while old miners will mine a separate chain based on the old rules. The partitioned network will make it so that the miners operating on separate consensus rules won’t likely receive each other’s blocks, as they are connected to two separate networks.
Diverging miners and difficulty
As miners diverge into mining two different chains, the hashing power is split between the chains. The mining power can be split in any proportion between the two chains. The new rules may only be followed by a minority, or by the vast majority of the mining power.
Let’s assume, for example, an 80%–20% split, with the majority of the mining power using the new consensus rules. Let’s also assume that the fork occurs immediately after a retargeting period.
The two chains would each inherit the difficulty from the retargeting period. The new consensus rules would have 80% of the previously available mining power committed to them. From the perspective of this chain, the mining power has suddenly declined by 20% vis-a-vis the previous period. Blocks will be found on average every 12.5 minutes, representing the 20% decline in mining power available to extend this chain. This rate of block issuance will continue (barring any changes in hashing power) until 2,016 blocks are mined, which will take approximately 25,200 minutes (at 12.5 minutes per block), or 17.5 days. After 17.5 days, a retarget will occur and the difficulty will adjust (reduced by 20%) to produce 10-minute blocks again, based on the reduced amount of hashing power in this chain.
The minority chain, mining under the old rules with only 20% of the hashing power, will face a much more difficult task. On this chain, blocks will now be mined every 50 minutes on average. The difficulty will not be adjusted for 2,016 blocks, which will take 100,800 minutes, or approximately 10 weeks to mine. Assuming a fixed capacity per block, this will also result in a reduction of transaction capacity by a factor of 5, as there are fewer blocks per hour available to record transactions.
Contentious hard forks
This is the dawn of the development of software for decentralized consensus. Just as other innovations in development changed both the methods and products of software and created new methodologies, new tools, and new communities in its wake, consensus software development also represents a new frontier in computer science. Out of the debates, experiments, and tribulations of Bitcoin development, we will see new development tools, practices, methodologies, and communities emerge.
Hard forks are seen as risky because they force a minority to either upgrade or remain on a minority chain. The risk of splitting the entire system into two competing systems is seen by many as an unacceptable risk. As a result, many developers are reluctant to use the hard fork mechanism to implement upgrades to the consensus rules, unless there is near-unanimous support from the entire network. Any hard fork proposals that do not have near-unanimous support are considered too contentious to attempt without risking a partition of the system.
Already we have seen the emergence of new methodologies to address the risks of hard forks. In the next section, we will look at soft forks and the methods for signaling and activation of consensus modifications.
Soft Forks
Not all consensus rule changes cause a hard fork. Only consensus changes that are forward-incompatible cause a fork. If the change is implemented in such a way that an unmodified client still sees the transaction or block as valid under the previous rules, the change can happen without a fork.
The term soft fork was introduced to distinguish this upgrade method from a "hard fork." In practice, a soft fork is not a fork at all. A soft fork is a forward-compatible change to the consensus rules that allows unupgraded clients to continue to operate in consensus with the new rules.
One aspect of soft forks that is not immediately obvious is that soft fork upgrades can only be used to constrain the consensus rules, not to expand them. In order to be forward compatible, transactions and blocks created under the new rules must be valid under the old rules too, but not vice versa. The new rules can only limit what is valid; otherwise, they will trigger a hard fork when rejected under the old rules.
Soft forks can be implemented in a number of ways—the term does not specify a particular method, but rather a set of methods that all have one thing in common: they don’t require all nodes to upgrade or force nonupgraded nodes out of consensus.
Two soft forks have been implemented in Bitcoin, based on the re-interpretation of NOP opcodes. Bitcoin Script had 10 opcodes reserved for future use, NOP1 through NOP10. Under the consensus rules, the presence of these opcodes in a script is interpreted as a null-potent operator, meaning they have no effect. Execution continues after the NOP opcode as if it wasn’t there.
A soft fork therefore can modify the semantics of a NOP code to give it new meaning. For example, BIP65 (CHECKLOCKTIMEVERIFY) reinterpreted the NOP2 opcode. Clients implementing BIP65 interpret NOP2 as OP_CHECKLOCKTIMEVERIFY and impose an absolute lock time consensus rule on UTXOs that contain this opcode in their locking scripts. This change is a soft fork because a transaction that is valid under BIP65 is also valid on any client that is not implementing (ignorant of) BIP65. To the old clients, the script contains an NOP code, which is ignored.
Criticisms of soft forks
Soft forks based on the NOP opcodes are relatively uncontroversial. The NOP opcodes were placed in Bitcoin Script with the explicit goal of allowing non-disruptive upgrades.
However, many developers are concerned that other methods of soft fork upgrades make unacceptable trade-offs. Common criticisms of soft fork changes include:
- Technical debt
-
Because soft forks are more technically complex than a hard fork upgrade, they introduce technical debt, a term that refers to increasing the future cost of code maintenance because of design trade-offs made in the past. Code complexity in turn increases the likelihood of bugs and security vulnerabilities.
- Validation relaxation
-
Unmodified clients see transactions as valid without evaluating the modified consensus rules. In effect, the unmodified clients are not validating using the full range of consensus rules, as they are blind to the new rules. This applies to NOP-based upgrades, as well as other soft fork upgrades.
- Irreversible upgrades
-
Because soft forks create transactions with additional consensus constraints, they become irreversible upgrades in practice. If a soft fork upgrade were to be reversed after being activated, any transactions created under the new rules could result in a loss of funds under the old rules. For example, if a CLTV transaction is evaluated under the old rules, there is no timelock constraint and it can be spent at any time. Therefore, critics contend that a failed soft fork that had to be reversed because of a bug would almost certainly lead to loss of funds.
Soft fork signaling with block version
Since soft forks allow unmodified clients to continue to operate within consensus, one mechanism for "activating" a soft fork is through miners signaling that they are ready and willing to enforce the new consensus rules. If all miners enforce the new rules, there’s no risk of unmodified nodes accepting a block that upgraded nodes would reject. This mechanism was introduced by BIP34.
BIP34: Signaling and activation
BIP34 used the block version field to allow miners to signal readiness for a specific consensus rule change. Prior to BIP34, the block version was set to "1" by convention not enforced by consensus.
BIP34 defined a consensus rule change that required the coinbase field (input) of the coinbase transaction to contain the block height. Prior to BIP34, the coinbase could contain any arbitrary data the miners chose to include. After activation of BIP34, valid blocks had to contain a specific block height at the beginning of the coinbase and be identified with a block version number greater than or equal to "2."
To signal their readiness to enforce the rules of BIP34, miners set the block version to "2," instead of "1." This did not immediately make version "1" blocks invalid. Once activated, version "1" blocks would become invalid and all version "2" blocks would be required to contain the block height in the coinbase to be valid.
BIP34 defined a two-step activation mechanism based on a rolling window of 1,000 blocks. A miner would signal their individual readiness for BIP34 by constructing blocks with "2" as the version number. Strictly speaking, these blocks did not yet have to comply with the new consensus rule of including the block height in the coinbase transaction because the consensus rule had not yet been activated. The consensus rules activated in two steps:
-
If 75% (750 of the most recent 1,000 blocks) are marked with version "2," then version "2" blocks must contain block height in the coinbase transaction or they are rejected as invalid. Version "1" blocks are still accepted by the network and do not need to contain block height. The old and new consensus rules coexist during this period.
-
When 95% (950 of the most recent 1,000 blocks) are version "2," version "1" blocks are no longer considered valid. Version "2" blocks are valid only if they contain the block height in the coinbase (as per the previous threshold). Thereafter, all blocks must comply with the new consensus rules, and all valid blocks must contain block height in the coinbase transaction.
After successful signaling and activation under the BIP34 rules, this mechanism was used twice more to activate soft forks:
After the activation of BIP65, the signaling and activation mechanism of BIP34 was retired and replaced with the BIP9 signaling mechanism described next.
BIP9: Signaling and activation
The mechanism used by BIP34, BIP66, and BIP65 was successful in activating three soft forks. However, it was replaced because it had several limitations:
-
By using the integer value of the block version, only one soft fork could be activated at a time, so it required coordination between soft fork proposals and agreement on their prioritization and sequencing.
-
Furthermore, because the block version was incremented, the mechanism didn’t offer a straightforward way to reject a change and then propose a different one. If old clients were still running, they could mistake signaling for a new change as signaling for the previously rejected change.
-
Each new change irrevocably reduced the available block versions for future changes.
BIP9 was proposed to overcome these challenges and improve the rate and ease of implementing future changes.
BIP9 interprets the block version as a bit field instead of an integer. Because the block version was originally used as an integer for versions 1 through 4, only 29 bits remain available to be used as a bit field. This leaves 29 bits that can be used to independently and simultaneously signal readiness on 29 different proposals.
BIP9 also sets a maximum time for signaling and activation. This way miners don’t need to signal forever. If a proposal is not activated within the TIMEOUT period (defined in the proposal), the proposal is considered rejected. The proposal may be resubmitted for signaling with a different bit, renewing the activation period.
Furthermore, after the TIMEOUT has passed and a feature has been activated or rejected, the signaling bit can be reused for another feature without confusion. Therefore, up to 29 changes can be signaled in parallel. After TIMEOUT, the bits can be "recycled" to propose new changes.
|
Note
|
While signaling bits can be reused or recycled, as long as the voting period does not overlap, the authors of BIP9 recommend that bits are reused only when necessary; unexpected behavior could occur due to bugs in older software. In short, we should not expect to see reuse until all 29 bits have been used once. |
Proposed changes are identified by a data structure that contains the following fields:
- name
-
A short description used to distinguish between proposals. Most often the BIP describing the proposal, as "bipN," where N is the BIP number.
- bit
-
0 through 28, the bit in the block version that miners use to signal approval for this proposal.
- starttime
-
The time (based on MTP) that signaling starts after which the bit’s value is interpreted as signaling readiness for the proposal.
- endtime
-
The time (based on MTP) after which the change is considered rejected if it has not reached the activation threshold.
Unlike BIP34, BIP9 counts activation signaling in whole intervals based on the difficulty retarget period of 2,016 blocks. For every retarget period, if the sum of blocks signaling for a proposal exceeds 95% (1,916 of 2,016), the proposal will be activated one retarget period later.
BIP9 offers a proposal state diagram to illustrate the various stages and transitions for a proposal, as shown in BIP9 state transition diagram..
Proposals start in the DEFINED state once their parameters are known (defined) in the Bitcoin software. For blocks with MTP after the start time, the proposal state transitions to STARTED. If the voting threshold is exceeded within a retarget period and the timeout has not been exceeded, the proposal state transitions to LOCKED_IN. One retarget period later, the proposal becomes ACTIVE. Proposals remain in the ACTIVE state perpetually once they reach that state. If the timeout elapses before the voting threshold has been reached, the proposal state changes to FAILED, indicating a rejected proposal. FAILED proposals remain in that state perpetually.
BIP9 was first implemented for the activation of CHECKSEQUENCEVERIFY and associated BIPs (68, 112, 113). The proposal named "csv" was activated successfully in July of 2016.
The standard is defined in BIP9 (Version bits with timeout and delay).
BIP8: Mandatory lock-in with early activation
After BIP9 was successfully used for the CSV-related soft fork, the next implementation of a soft fork consensus change also attempted to use it for miner-enforced activation. However, some people opposed that soft fork proposal, called segwit, and very few miners signaled readiness to enforce segwit for several months.
It was later discovered that some miners, especially miners associated with the dissenters, may have been using hardware that gave them a hidden advantage over other miners using a feature called covert ASICBoost. Unintentionally, segwit interfered with the ability to use covert ASICBoost—if segwit was activated, the miners using it would lose their hidden advantage.
After the community discovered this conflict of interest, some users decided they wanted to exercise their power not to accept blocks from miners unless those blocks followed certain rules. The rules the users ultimately wanted were the new rules added by segwit, but the users wanted to multiply their efforts by taking advantage of the large numbers of nodes that planned to enforce the rules of segwit if enough miners signaled readiness for it. A pseudonymous developer proposed BIP148, which required any node implementing it to reject all blocks that didn’t signal for segwit starting on a certain date and continuing until segwit activated.
Although only a limited number of users actually ran BIP148 code, many other users seemed to agree with the sentiment and may have been prepared to commit to BIP148. A few days before BIP148 was due to go into effect, almost all miners began signaling their readiness to enforce segwit’s rules. Segwit reached its lock-in threshold about two weeks later and activated about two weeks after that.
Many users came to believe that it was a flaw in BIP9 that miners could prevent an activation attempt from being successful by not signaling for a year. They wanted a mechanism that would ensure a soft fork was activated by a particular block height but which also allowed miners to signal they were ready to lock it in earlier.
The method developed for that was BIP8, which is similar to BIP9 except that it defines a MUST_SIGNAL period where miners must signal that they are ready to enforce the soft fork proposal.
Software was published that used BIP8 to attempt to activate the taproot proposal in 2021, and there was evidence that at least a small number of users ran that software. Some of those users also claim that their willingness to use BIP8 to force miners to activate taproot was the reason it did eventually activate. They claim that if taproot had not been activated quickly, other users would have also begun running BIP8. Unfortunately, there’s no way to prove what would have happened, and so we can’t say for sure how much BIP8 contributed to the activation of taproot.
Speedy trial: Fail fast or succeed eventually
Although BIP9 by itself did not seem to result in the activation of segwit despite widespread support for the proposal, it was unclear to many protocol developers that BIP9 was itself a failure. As mentioned, the failure of miners to initially signal support for segwit may have been largely the result of a one-time conflict of interest that wouldn’t apply in the future. To some, it seemed worth trying BIP9 again. Others disagreed and wanted to use BIP8.
After months of discussions between those who were the most interested in specific activation ideas, a compromise was suggested in order to activate taproot. A modified version of BIP9 was suggested that would only give miners a very short amount of time to signal their intention to enforce taproot rules. If signaling was unsuccessful, a different activation mechanism could be used (or, potentially, the idea could be abandoned). If signaling was successful, enforcement would begin about six months later at a specified block height. This mechanism was named speedy trial by one of the people who helped promote it.
Speedy trial activation was tried, miners quickly signaled their willingness to enforce the rules of taproot, and taproot was successfully activated about six months later. To proponents of speedy trial, it was a clear success. Others were still disappointed that BIP8 wasn’t used.
It’s not clear whether or not speedy trial will be used again for a future attempt to activate a soft fork.
Consensus Software Development
Consensus software continues to evolve, and there is much discussion on the various mechanisms for changing the consensus rules. By its very nature, Bitcoin sets a very high bar on coordination and consensus for changes. As a decentralized system, it has no "authority" that can impose its will on the participants of the network. Power is diffused between multiple constituencies such as miners, protocol developers, wallet developers, exchanges, merchants, and end users. Decisions cannot be made unilaterally by any of these constituencies. For example, while miners can censor transactions by simple majority (51%), they are constrained by the consent of the other constituencies. If they act unilaterally, the rest of the participants may refuse to accept their blocks, keeping the economic activity on a minority chain. Without economic activity (transactions, merchants, wallets, exchanges), the miners will be mining a worthless currency with empty blocks. This diffusion of power means that all the participants must coordinate, or no changes can be made. Status quo is the stable state of this system with only a few changes possible if there is strong consensus by a very large majority. The 95% threshold for soft forks is reflective of this reality.
It is important to recognize that there is no perfect solution for consensus development. Both hard forks and soft forks involve trade-offs. For some types of changes, soft forks may be a better choice; for others, hard forks may be a better choice. There is no perfect choice; both carry risks. The one constant characteristic of consensus software development is that change is difficult and consensus forces compromise.
Some see this as a weakness of consensus systems. In time, you may come to see it as the system’s greatest strength.
At this point in the book, we’ve finished talking about the Bitcoin system itself. What’s left are software, tools, and other protocols built on top of Bitcoin.